علم الكيمياء
تاريخ الكيمياء والعلماء المشاهير
التحاضير والتجارب الكيميائية
المخاطر والوقاية في الكيمياء
اخرى
مقالات متنوعة في علم الكيمياء
كيمياء عامة
الكيمياء التحليلية
مواضيع عامة في الكيمياء التحليلية
التحليل النوعي والكمي
التحليل الآلي (الطيفي)
طرق الفصل والتنقية
الكيمياء الحياتية
مواضيع عامة في الكيمياء الحياتية
الكاربوهيدرات
الاحماض الامينية والبروتينات
الانزيمات
الدهون
الاحماض النووية
الفيتامينات والمرافقات الانزيمية
الهرمونات
الكيمياء العضوية
مواضيع عامة في الكيمياء العضوية
الهايدروكاربونات
المركبات الوسطية وميكانيكيات التفاعلات العضوية
التشخيص العضوي
تجارب وتفاعلات في الكيمياء العضوية
الكيمياء الفيزيائية
مواضيع عامة في الكيمياء الفيزيائية
الكيمياء الحرارية
حركية التفاعلات الكيميائية
الكيمياء الكهربائية
الكيمياء اللاعضوية
مواضيع عامة في الكيمياء اللاعضوية
الجدول الدوري وخواص العناصر
نظريات التآصر الكيميائي
كيمياء العناصر الانتقالية ومركباتها المعقدة
مواضيع اخرى في الكيمياء
كيمياء النانو
الكيمياء السريرية
الكيمياء الطبية والدوائية
كيمياء الاغذية والنواتج الطبيعية
الكيمياء الجنائية
الكيمياء الصناعية
البترو كيمياويات
الكيمياء الخضراء
كيمياء البيئة
كيمياء البوليمرات
مواضيع عامة في الكيمياء الصناعية
الكيمياء الاشعاعية والنووية
الأضـداد الضوئية
المؤلف:
أ. د محمد مجدي واصل
المصدر:
اساسيات الكيمياء العضوية
الجزء والصفحة:
ص 172-173-174-175
2023-08-07
1189
لقد أقتصر شرحنا سابقاً على جزئيات حاوية على ذرة كاربون كيرالية واحدة بينما هناك عدد كبير من المركبات العضوية الحاوية على أكثر من ذرة كابرون كيرالية وللسهولة سوف نبدأ بمركب حاو على ذرتي كاربون كيرالية مختلفتين مثل 2 ، 3 - ثنائي كلورو – بنتان .
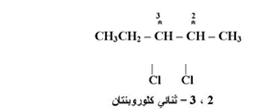
والآن ما عدد المتشكلات الفراغية المتوقعة لهذا المركب ؟ فنجد أن هناك قاعدة تمكننا من حساب عدد المتشكلات الفراغية وهي أن العدد الكلي المتشكلات الفراغية لا يتجاوز ( N2 ) حيث أن ( ن ) تمثل عدد ذرات الكاربون الكيرالية ولذلك نتوقع للصيغة المبينة أعلاه عددا من المتشكلات الفراغية لا يزيد عن ( 22 = 4 ).
ولغرض الوقوف على طبيعة الصيغ المجسمة للمتشكلات الفراغية لهذا المركب سوف نحاول رسم صيغة مجسمة لمتشكل فراغي وصيغة أخرى لصورة مرأه له ( أ و ب ) وذلك كما يلي :
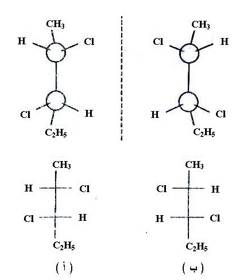
وبما أن البنائين أ و ب ليسا متطابقين لذلك يعدان مركبين مختلفين وهما يختلفان فقط في توزيع الذرات في الفراغ أي أنهما متشكلات فراغيان إضافة إلى ذلك فهما كالجسم وصورته في المرآة لذلك يعدان ندين ضوئيان حيث أن كل واحد منهما له القابلية على إظهار نشاط ضوئي .
إلا أن البناءين ( أ و ب ) ليسا الوحيدان ، فيمكن كتابة البناء (ج) الذي يختلف من كل من ( أ و ب ) ونستطيع كذلك أن نكتب صورة مرأة (د) لبناء (ج) لا تتطابق معه فهما إذا ندان آخران ، فإذا حاولنا أن نرسم بناءات أخرى من خلال الدوران حول الروابط المنفردة أو دوران البناء ككل فأننا سوف نحصل على بناء يتطابق مع واحد من الأربعة التي رسمت ( أ - د ).
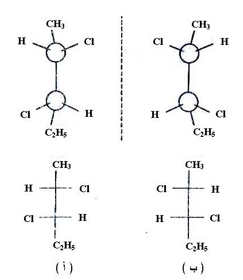
أن المتشكلات أ - د كانت جميعها مختلفة حيث أنها تمثل الحد الأقصى من المتشكلات الفراغية التي يمكن رسمها لهذا المركب وأن جميعها متشكلات تشطة ضوئيا ولذى ما العلاقة بين المتشكلات الأربع ؟
فعند الرجوع إلى الصيغ البنائية لهذه المتشكلات ( أ - د ) نجد هناك ملاحظتان مهمتان الأولى هي وجود زوجان من المتشكلات ( أ - ب ) و (ج - د ) . وإن كل زوج منهما كالجسم وصورته في مرآة والملاحظة الثانية هي أننا لو قارنا الزوجين ( أ ، د ) و ( ب ، ج ) لوجدنا بأنهما كذلك متشكلات فراغية إلا أنها ليستا كالجسم وصورته في مرأة فهما إذا ضدين ضوئيين أو دياستير يومرات فهما يختلفان في الخواص الفيزيائية كدرجات الانصهار والغليان والذائبية وغيرها لذلك لا يعدان ندين ضوئين .
إستعراض موجز لحياة السيدة زينب الكبرى
أم البنين .. صانعة الوفاء وراعية الفضيلة
هل كان الشيخ الوائلي يعلم؟!
