
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Speed
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 8
2024-02-04
1828
Even though we know roughly what “speed” means, there are still some rather deep subtleties; consider that the learned Greeks were never able to adequately describe problems involving velocity. The subtlety comes when we try to comprehend exactly what is meant by “speed.” The Greeks got very confused about this, and a new branch of mathematics had to be discovered beyond the geometry and algebra of the Greeks, Arabs, and Babylonians. As an illustration of the difficulty, try to solve this problem by sheer algebra: A balloon is being inflated so that the volume of the balloon is increasing at the rate of 100 cm³ per second; at what speed is the radius increasing when the volume is 1000 cm³? The Greeks were somewhat confused by such problems, being helped, of course, by some very confusing Greeks. To show that there were difficulties in reasoning about speed at the time, Zeno produced a large number of paradoxes, of which we shall mention one to illustrate his point that there are obvious difficulties in thinking about motion. “Listen,” he says, “to the following argument: Achilles runs 10 times as fast as a tortoise, nevertheless he can never catch the tortoise. For, suppose that they start in a race where the tortoise is 100 meters ahead of Achilles; then when Achilles has run the 100 meters to the place where the tortoise was, the tortoise has proceeded 10 meters, having run one-tenth as fast. Now, Achilles has to run another 10 meters to catch up with the tortoise, but on arriving at the end of that run, he finds that the tortoise is still 1 meter ahead of him; running another meter, he finds the tortoise 10 centimeters ahead, and so on, ad infinitum. Therefore, at any moment the tortoise is always ahead of Achilles and Achilles can never catch up with the tortoise.” What is wrong with that? It is that a finite amount of time can be divided into an infinite number of pieces, just as a length of line can be divided into an infinite number of pieces by dividing repeatedly by two. And so, although there are an infinite number of steps (in the argument) to the point at which Achilles reaches the tortoise, it doesn’t mean that there is an infinite amount of time. We can see from this example that there are indeed some subtleties in reasoning about speed.
In order to get to the subtleties in a clearer fashion, we remind you of a joke which you surely must have heard. At the point where the lady in the car is caught by a cop, the cop comes up to her and says, “Lady, you were going 60 miles an hour!” She says, “That’s impossible, sir, I was travelling for only seven minutes. It is ridiculous—how can I go 60 miles an hour when I wasn’t going an hour?” How would you answer her if you were the cop? Of course, if you were really the cop, then no subtleties are involved; it is very simple: you say, “Tell that to the judge!” But let us suppose that we do not have that escape and we make a more honest, intellectual attack on the problem, and try to explain to this lady what we mean by the idea that she was going 60 miles an hour. Just what do we mean? We say, “What we mean, lady, is this: if you kept on going the same way as you are going now, in the next hour you would go 60 miles.” She could say, “Well, my foot was off the accelerator and the car was slowing down, so if I kept on going that way it would not go 60 miles.” Or consider the falling ball and suppose we want to know its speed at the time three seconds if the ball kept on going the way it is going. What does that mean—kept on accelerating, going faster? No—kept on going with the same velocity. But that is what we are trying to define! For if the ball keeps on going the way it is going, it will just keep on going the way it is going. Thus, we need to define the velocity better. What has to be kept the same? The lady can also argue this way: “If I kept on going the way I’m going for one more hour, I would run into that wall at the end of the street!” It is not so easy to say what we mean.
Many physicists think that measurement is the only definition of anything. Obviously, then, we should use the instrument that measures the speed—the speedometer—and say, “Look, lady, your speedometer reads 60.” So, she says, “My speedometer is broken and didn’t read at all.” Does that mean the car is standing still? We believe that there is something to measure before we build the speedometer. Only then can we say, for example, “The speedometer isn’t working right,” or “the speedometer is broken.” That would be a meaningless sentence if the velocity had no meaning independent of the speedometer. So we have in our minds, obviously, an idea that is independent of the speedometer, and the speedometer is meant only to measure this idea. So let us see if we can get a better definition of the idea. We say, “Yes, of course, before you went an hour, you would hit that wall, but if you went one second, you would go 88 feet; lady, you were going 88 feet per second, and if you kept on going, the next second it would be 88 feet, and the wall down there is farther away than that.” She says, “Yes, but there’s no law against going 88 feet per second! There is only a law against going 60 miles an hour.” “But,” we reply, “it’s the same thing.” If it is the same thing, it should not be necessary to go into this circumlocution about 88 feet per second. In fact, the falling ball could not keep going the same way even one second because it would be changing speed, and we shall have to define speed somehow.
Now we seem to be getting on the right track; it goes something like this: If the lady kept on going for another 1/1000 of an hour, she would go 1/1000 of 60 miles. In other words, she does not have to keep on going for the whole hour; the point is that for a moment she is going at that speed. Now what that means is that if she went just a little bit more in time, the extra distance she goes would be the same as that of a car that goes at a steady speed of 60 miles an hour. Perhaps the idea of the 88 feet per second is right; we see how far she went in the last second, divide by 88 feet, and if it comes out 1 the speed was 60 miles an hour. In other words, we can find the speed in this way: We ask, how far do we go in a very short time? We divide that distance by the time, and that gives the speed. But the time should be made as short as possible, the shorter the better, because some change could take place during that time. If we take the time of a falling body as an hour, the idea is ridiculous. If we take it as a second, the result is pretty good for a car, because there is not much change in speed, but not for a falling body; so in order to get the speed more and more accurately, we should take a smaller and smaller time interval. What we should do is take a millionth of a second, find out how far the car has gone, and divide that distance by a millionth of a second. The result gives the distance per second, which is what we mean by the velocity, so we can define it that way. That is a successful answer for the lady, or rather, that is the definition that we are going to use.
The foregoing definition involves a new idea, an idea that was not available to the Greeks in a general form. That idea was to take an infinitesimal distance and the corresponding infinitesimal time, form the ratio, and watch what happens to that ratio as the time that we use gets smaller and smaller and smaller. In other words, take a limit of the distance travelled divided by the time required, as the time taken gets smaller and smaller, ad infinitum. This idea was invented by Newton and by Leibniz, independently, and is the beginning of a new branch of mathematics, called the differential calculus. Calculus was invented in order to describe motion, and its first application was to the problem of defining what is meant by going “60 miles an hour.”
Let us try to define velocity a little better. Suppose that in a short time, ϵ, the car or other body goes a short distance x; then the velocity, v, is defined as
v=x/ϵ,
an approximation that becomes better and better as the ϵ is taken smaller and smaller. If a mathematical expression is desired, we can say that the velocity equals the limit as the ϵ is made to go smaller and smaller in the expression x/ϵ, or
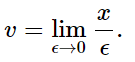
We cannot do the same thing with the lady in the car, because the table is incomplete. We know only where she was at intervals of one minute; we can get a rough idea that she was going 5000 ft/min during the 7th minute, but we do not know, at exactly the moment 7 minutes, whether she had been speeding up and the speed was 4900 ft/min at the beginning of the 6th minute, and is now 5100 ft/min, or something else, because we do not have the exact details in between. So only if the table were completed with an infinite number of entries could we really calculate the velocity from such a table. On the other hand, when we have a complete mathematical formula, as in the case of a falling body (Eq. 8.1), then it is possible to calculate the velocity, because we can calculate the position at any time whatsoever.
Let us take as an example the problem of determining the velocity of the falling ball at the particular time 5 seconds. One way to do this is to see from Table 8–2 what it did in the 5th second; it went 400−256=144 ft, so it is going 144 ft/sec; however, that is wrong, because the speed is changing; on the average it is 144 ft/sec during this interval, but the ball is speeding up and is really going faster than 144 ft/sec. We want to find out exactly how fast. The technique involved in this process is the following: We know where the ball was at 5 sec. At 5.1 sec, the distance that it has gone all together is 16(5.1)2=416.16 ft (see Eq. 8.1). At 5 sec it had already fallen 400 ft; in the last tenth of a second it fell 416.16−400=16.16 ft. Since 16.16 ft in 0.1 sec is the same as 161.6 ft/sec, that is the speed more or less, but it is not exactly correct. Is that the speed at 5, or at 5.1, or halfway between at 5.05 sec, or when is that the speed? Never mind—the problem was to find the speed at 5 seconds, and we do not have exactly that; we have to do a better job. So, we take one-thousandth of a second more than 5 sec, or 5.001 sec, and calculate the total fall as
s=16(5.001)2= 16(25.010001)
= 400.160016 ft.
In the last 0.001 sec the ball fell 0.160016 ft, and if we divide this number by 0.001 sec we obtain the speed as 160.016 ft/sec. That is closer, very close, but it is still not exact. It should now be evident what we must do to find the speed exactly. To perform the mathematics, we state the problem a little more abstractly: to find the velocity at a special time, t0, which in the original problem was 5 sec. Now the distance at t0, which we call s0, is 16 t20, or 400 ft in this case. In order to find the velocity, we ask, “At the time t0 + (a little bit), or t0 + ϵ, where is the body?” The new position is 16(t0+ϵ)2=16t20+32t0ϵ+16ϵ2. So, it is farther along than it was before, because before it was only 16t20. This distance we shall call s0+(a little bit more), or s0+x (if x is the extra bit). Now if we subtract the distance at t0 from the distance at t0+ϵ, we get x, the extra distance gone, as x=32t0⋅ϵ+16ϵ2. Our first approximation to the velocity is
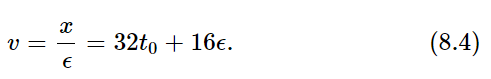
The true velocity is the value of this ratio, x/ϵ, when ϵ becomes vanishingly small. In other words, after forming the ratio, we take the limit as ϵ gets smaller and smaller, that is, approaches 0. The equation reduces to,
v (at time t0) = 32t0.
In our problem, t0=5 sec, so the solution is v= 32×5= 160 ft/sec. A few lines above, where we took ϵ as 0.1 and 0.001 sec successively, the value we got for v was a little more than this, but now we see that the actual velocity is precisely 160 ft/sec.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















