البندول البسيط

نحن نعلم أن أي بندول بسيط كالمبين بالشكل 1)) يتذبذب في حركة دورية , فإذا أمكن إثبات أن قوة الاستعادة تتناسب طرديا مع الإزاحة عن موضعا الاتزان فإننا نستنتج أن البندول يتحرك حركة توافقية بسيطة.

ومن المعلوم أيضا أن البندول يكون في موضع الاتزان عندما يكون الخيط رأسيا. وإذا أزيح البندول من موضع الاتزان بحيث يصنع الخطي زاوية θ مع الرأسي , كما هو مبين بالشكل 1)) ،

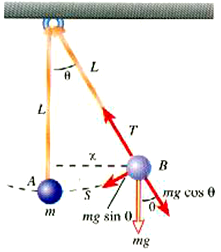
الشكل (1): البندول البسيط. قوة الاستعادة هي mg sin θ = mg θ. لاحظ أن θ = s/L حيث s طول القوس بين النقطتين  A و B.

سوف نجد أن هناك قوتين مؤثرتين على الكتلة m  هما: الشد T هو يؤثر على استقامة الخيط في اتجاه نقطة التعليق دائما , والوزنmg  ويؤثر رأسيا الى أسفل دائما. ومن الواضح أن صافي القوة نصف القطرية على استقامة الخيط (T – mg cos θ)  يجبر الكتلة m  على الحركة على قوس دائري نصف قطره يساوي طول البندول L. أما المركبة المماسية للوزنmg  وتساويmg sin θ  تؤثر دائما على استقامة قوس الدائرة تجاه نقطة الاتزان. وعليه يمكننا كتابة:

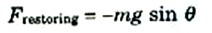
حيث تبين الإشارة السالبة أن القوة في عكس اتجاه زيادة θ. ولكن في حالة الزوايا الصغيرة يمكننا استخدام حقيقة أن sin θ ≈ θ ، حيث θ مقدرة بالزوايا نصف القطرية. (هذا التقريب يكون مضبوطا الى ثلاثة أرقام معنوية إذا كانت  ≤ 10^oθ، اي 0.174 rad ) ومن تعريف القياس نصف القطر للزوايا يمكننا أيضا كتابة  = s/L = x/Lθ. ومن ثم سوف تأخذ قوة الاستعادة الصورة:

وهي صورة للعلاقة بين القوة والإزاحة في حالة SHM .

وبمقارنة هذه المعادلة بالصيغة العامة F = -kx  نجد مباشرة أن:

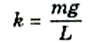
ومنه يمكن الحصول مباشرة على تردد اهتزاز  البندول:

  1))         

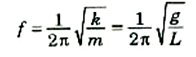
لاحظ أن تردد البندول البسيط لا يعتمد على كتلة البندول , ولكنه يعتمد فقط على الطول L عجلة الجاذبية g. وبالرغم من بساطة هذه النتيجة إلا أنها تمثل طريقة دقيقة لقياس g , ويمكن تحقيق ذلك بقيام متوسط الزمن الدوري لبندول معلوم الطول  ثم استخدامه لحساب التردد f ثم التعويض في المعادلة (1) لحساب g.

ومن الممكن كتابة معادلة حركة البندول كالتالي :

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل