
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الشغل المنجز من قبل قوة النابض (Work Done by Spring Force)
المؤلف:
د. معن صفاء ابراهيم
المصدر:
الفيزياء الجامعية 101
الجزء والصفحة:
ص 145
19-2-2016
43316
الشغل المنجز من قبل قوة النابض (Work Done by Spring Force)
النابض هو سلك ملتوي (حلزوني) له مرونة معينة تعتمد على نوع المادة المصنوع منها وبذلك يمكن سحبه أو ضغطه إلى حدود معينة تعتمد على درجة مرونته. وعند ضغط أو سحب النابض تتولد قوة تحاول إعاقة السحب أو الضغط وتتجه دائماً باتجاه نقطة استقرار النابض (equilibrium position) وتسمى بقوة إرجاع النابض (restoring force) ويمكن إيجاد قيمتها استناداً إلى قانون هوك:
Fs = - kx
حيث Fs تمثل قوة إرجاع النابض، x تمثل مقدار إزاحة النابض عن نقطة الاستقرار (خلال الضغط أو السحب)، اما k فتمثل ثابت مرونة او صلابة النابض، وتكون قيمته صغيرة في أنواع النابض المرن، وكبيرة في انواع النابض الصلب، الإشارة السالبة في قانون هوك تشير إلى إن اتجاه القوة دائماً يعاكس اتجاه الإزاحة التي يقطعها النابض، إن قوة إرجاع النابض هي قوة متغيرة تعتمد قيمتها على مقدار السحب أو الضغط الذي يتعرض له النابض، ولذلك يستخدم قانون التكامل المحدود لإيجاد الشغل الناتج عن قوة إرجاع النابض. وكمثال على ذلك نتصور حالة جسم مرتبط بنابض وهو في حالة ضغط كما في الشكل (1-1)، وعند ترك النابض حر الحركة سوف يندفع الجسم بفعل قوة إرجاع النابض التي تولدت فيتحرك النابض من الموقع xi = -xm إلى الموقع xf = xm ماراً بنقطة الاستقرار x = 0.

الشكل (1-1)
ولإيجاد الشغل المنجز على الجسم من قبل قوة إرجاع النابض من النقطة xi = -xm إلى نقطة الاستقرار x = 0، نستخدم القانون التالي:
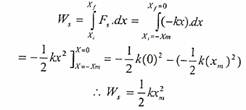
أي أن الشغل موجب.
ولإيجاد الشغل المنجز على الجسم من نقطة الاستقرار إلى الموقع xf = xm نستخدم القانون التالي:
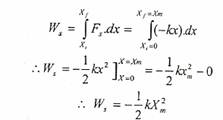
أي أن الشغل سالب. وفي حالة تساوي xm مع -xm فإن الشغل الكلي المنجز على الجسم من xi = -xm إلى xf = xm سوف يساوي صفراً.
ومن الممكن أن نلجئ إلى حفظ صيغة عامة للشغل المنجز من قبل قوة إرجاع النابض ولأي إزاحة كانت بحيث نستعيض عن إجراء التكامل المحدود وكما يلي:
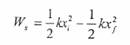
وبالتعويض عن قيمة إحداثي الموقع (x) الأولى والنهائي للنابض يمكن إيجاد الشغل بسهولة دون الحاجة لإجراء التكامل المحدود. ومن المفيد أن نذكر أن قوة إرجاع النابض تساوي قيمة القوة التي تقوم بضغط او سحب النابض (Applied Force) ولكنها تعاكسها بالاتجاه حيث : Fapp = -Fs
ولذلك إذا كان المطلوب إيجاد الشغل من قبل القوة المسلطة على النابض Fapp ، فيمكن استخدام نفس القوانين السابقة مسبوقة بإشارة سالبة حيث : Wapp = -Ws
وبذلك يكون القانون العام كما يلي:
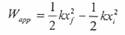
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















