
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Gravitational field of large objects
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 13
2024-02-14
1848
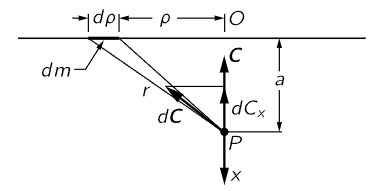
Fig. 13–5. The gravitational field C at a mass point produced by an infinite plane sheet of matter.
Now we shall calculate the fields which are met in a few physical circumstances involving distributions of mass. We have not so far considered distributions of mass, only particles, so it is interesting to calculate the forces when they are produced by more than just one particle. First, we shall find the gravitational force on a mass that is produced by a plane sheet of material, infinite in extent. The force on a unit mass at a given point P, produced by this sheet of material (Fig. 13–5), will of course be directed toward the sheet. Let the distance of the point from the sheet be a, and let the amount of mass per unit area of this huge sheet be μ. We shall suppose μ to be constant; it is a uniform sheet of material. Now, what small field dC is produced by the mass dm lying between ρ and ρ+dρ from the point O of the sheet nearest point P? Answer: dC=−G(dmr/r3). But this field is directed along r, and we know that only the x-component of it will remain when we add all the little vector dC’s to produce C. The x-component of dC is
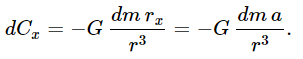
Now all masses dm which are at the same distance r from P will yield the same dCx, so we may at once write for dm the total mass in the ring between ρ and ρ+dρ, namely dm=μ2πρ dρ (2πρ dρ is the area of a ring of radius ρ and width dρ, if dρ≪ρ). Thus
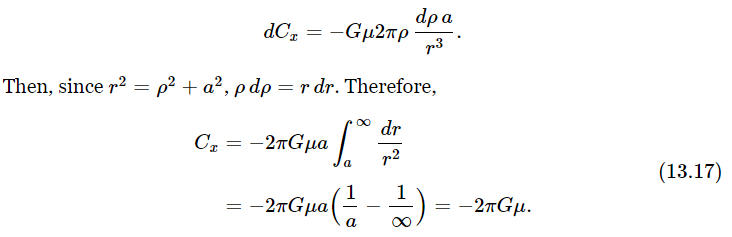
Thus the force is independent of distance a! Why? Have we made a mistake? One might think that the farther away we go, the weaker the force would be. But no! If we are close, most of the matter is pulling at an unfavorable angle; if we are far away, more of the matter is situated more favorably to exert a pull toward the plane. At any distance, the matter which is most effective lies in a certain cone. When we are farther away the force is smaller by the inverse square, but in the same cone, in the same angle, there is much more matter, larger by just the square of the distance! This analysis can be made rigorous by just noticing that the differential contribution in any given cone is in fact independent of the distance, because of the reciprocal variation of the strength of the force from a given mass, and the amount of mass included in the cone, with changing distance. The force is not really constant of course, because when we go on the other side of the sheet it is reversed in sign.
We have also, in effect, solved an electrical problem: if we have an electrically charged plate, with an amount σ of charge per unit area, then the electric field at a point outside the sheet is equal to σ/2ϵ0, and is in the outward direction if the sheet is positively charged, and inward if the sheet is negatively charged. To prove this, we merely note that −G, for gravity, plays the same role as 1/4πϵ0 for electricity.
Now suppose that we have two plates, with a positive charge +σ on one and a negative charge −σ on another at a distance D from the first. What is the field? Outside the two plates it is zero. Why? Because one attracts and the other repels, the force being independent of distance, so that the two balance out! Also, the field between the two plates is clearly twice as great as that from one plate, namely E=σ/ϵ0, and is directed from the positive plate to the negative one.
Now we come to a most interesting and important problem, whose solution we have been assuming all the time, namely, that the force produced by the earth at a point on the surface or outside it is the same as if all the mass of the earth were located at its center. The validity of this assumption is not obvious, because when we are close, some of the mass is very close to us, and some is farther away, and so on. When we add the effects all together, it seems a miracle that the net force is exactly the same as we would get if we put all the mass in the middle!
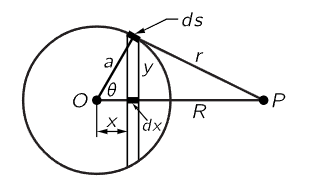
Fig. 13–6. A thin spherical shell of mass or charge.
We now demonstrate the correctness of this miracle. In order to do so, however, we shall consider a thin uniform hollow shell instead of the whole earth. Let the total mass of the shell be m, and let us calculate the potential energy of a particle of mass m′ a distance R away from the center of the sphere (Fig. 13–6) and show that the potential energy is the same as it would be if the mass m were a point at the center. (The potential energy is easier to work with than is the field because we do not have to worry about angles, we merely add the potential energies of all the pieces of mass.) If we call x the distance of a certain plane section from the center, then all the mass that is in a slice dx is at the same distance r from P, and the potential energy due to this ring is −Gm′dm/r. How much mass is in the small slice dx? An amount
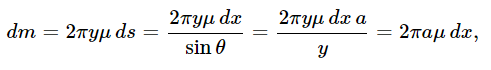
where μ=m/4πa2 is the surface density of mass on the spherical shell. (It is a general rule that the area of a zone of a sphere is proportional to its axial width.) Therefore, the potential energy due to dm is

Thus, for a thin spherical shell, the potential energy of a mass m′, external to the shell, is the same as though the mass of the shell were concentrated at its center. The earth can be imagined as a series of spherical shells, each one of which contributes an energy which depends only on its mass and the distance from its center to the particle; adding them all together we get the total mass, and therefore the earth acts as though all the material were at the center!
But notice what happens if our point is on the inside of the shell. Making the same calculation, but with P on the inside, we still get the difference of the two r’s, but now in the form a−R−(a+R)=−2R, or minus twice the distance from the center. In other words, W comes out to be W=−Gm′m/a, which is independent of R and independent of position, i.e., the same energy no matter where we are inside. Therefore, no force; no work is done when we move about inside. If the potential energy is the same no matter where an object is placed inside the sphere, there can be no force on it. So there is no force inside, there is only a force outside, and the force outside is the same as though the mass were all at the center.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















