
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Conservative forces
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 14
2024-02-15
1787
In nature there are certain forces, that of gravity, for example, which have a very remarkable property which we call “conservative” (no political ideas involved, it is again one of those “crazy words”). If we calculate how much work is done by a force in moving an object from one point to another along some curved path, in general the work depends upon the curve, but in special cases it does not. If it does not depend upon the curve, we say that the force is a conservative force. In other words, if the integral of the force times the distance in going from position 1 to position 2 in Fig. 14–2 is calculated along curve A and then along B, we get the same number of joules, and if this is true for this pair of points on every curve, and if the same proposition works no matter which pair of points we use, then we say the force is conservative. In such circumstances, the work integral going from 1 to 2 can be evaluated in a simple manner, and we can give a formula for the result. Ordinarily it is not this easy, because we also have to specify the curve, but when we have a case where the work does not depend on the curve, then, of course, the work depends only upon the positions of 1 and 2.
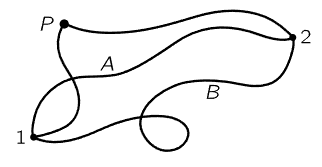
Fig. 14–2. Possible paths between two points in a field of force.
To demonstrate this idea, consider the following. We take a “standard” point P, at an arbitrary location (Fig. 14–2). Then, the work line-integral from 1 to 2, which we want to calculate, can be evaluated as the work done in going from 1 to P plus the work done in going from P to 2, because the forces are conservative and the work does not depend upon the curve. Now, the work done in going from position P to a particular position in space is a function of that position in space. Of course, it really depends on P also, but we hold the arbitrary point P fixed permanently for the analysis. If that is done, then the work done in going from point P to point 2 is some function of the final position of 2. It depends upon where 2 is; if we go to some other point, we get a different answer.
We shall call this function of position −U(x,y,z), and when we wish to refer to some particular point 2 whose coordinates are (x2,y2,z2), we shall write U(2), as an abbreviation for U(x2,y2,z2). The work done in going from point 1 to point P can be written also by going the other way along the integral, reversing all the ds’s. That is, the work done in going from 1 to P is minus the work done in going from the point P to 1A:
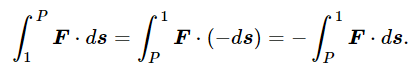
Thus the work done in going from P to 1 is −U(1), and from P to 2 the work is −U(2). Therefore the integral from 1 to 2 is equal to −U(2) plus [−U(1) backwards], or +U(1)−U(2):
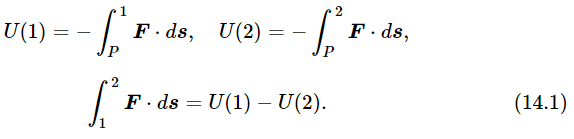
The quantity U(2)−U(1) is called the change in the potential energy, and we call U the potential energy. We shall say that when the object is located at position 2, it has potential energy U(2) and at position 1 it has potential energy U(1). If it is located at position P, it has zero potential energy. If we had used any other point, say Q, instead of P, it would turn out (and we shall leave it to you to demonstrate) that the potential energy is changed only by the addition of a constant. Since the conservation of energy depends only upon changes, it does not matter if we add a constant to the potential energy. Thus, the point P is arbitrary.
Now, we have the following two propositions: (1) that the work done by a force is equal to the change in kinetic energy of the particle, but (2) mathematically, for a conservative force, the work done is minus the change in a function U which we call the potential energy. As a consequence of these two, we arrive at the proposition that if only conservative forces act, the kinetic energy T plus the potential energy U remains constant:
T+U=constant. (14.2)
Let us now discuss the formulas for the potential energy for a number of cases. If we have a gravitational field that is uniform, if we are not going to heights comparable with the radius of the earth, then the force is a constant vertical force and the work done is simply the force times the vertical distance. Thus
U(z)=mgz, (14.3)
and the point P which corresponds to zero potential energy happens to be any point in the plane z=0. We could also have said that the potential energy is mg(z−6) if we had wanted to—all the results would, of course, be the same in our analysis except that the value of the potential energy at z=0 would be −6mg. It makes no difference, because only differences in potential energy count.
The energy needed to compress a linear spring a distance x from an equilibrium point is

and the zero of potential energy is at the point x=0, the equilibrium position of the spring. Again we could add any constant we wish.
The potential energy of gravitation for point masses M and m, a distance r apart, is

The constant has been chosen here so that the potential is zero at infinity. Of course, the same formula applies to electrical charges, because it is the same law:

Now let us actually use one of these formulas, to see whether we understand what it means. Question: How fast do we have to shoot a rocket away from the earth in order for it to leave? Solution: The kinetic plus potential energy must be a constant; when it “leaves,” it will be millions of miles away, and if it is just barely able to leave, we may suppose that it is moving with zero speed out there, just barely going. Let a be the radius of the earth, and M its mass. The kinetic plus potential energy is then initially given by 1/2 mv2−GmM/a. At the end of the motion the two energies must be equal. The kinetic energy is taken to be zero at the end of the motion, because it is supposed to be just barely drifting away at essentially zero speed, and the potential energy is GmM divided by infinity, which is zero. So, everything is zero on one side and that tells us that the square of the velocity must be 2GM/a. But GM/a2 is what we call the acceleration of gravity, g. Thus
v2=2ga.
At what speed must a satellite travel in order to keep going around the earth? We worked this out long ago and found that v2=GM/a. Therefore, to go away from the earth, we need √2 times the velocity we need to just go around the earth near its surface. We need, in other words, twice as much energy (because energy goes as the square of the velocity) to leave the earth as we do to go around it. Therefore, the first thing that was done historically with satellites was to get one to go around the earth, which requires a speed of five miles per second. The next thing was to send a satellite away from the earth permanently; this required twice the energy, or about seven miles per second.
Now, continuing our discussion of the characteristics of potential energy, let us consider the interaction of two molecules, or two atoms, two oxygen atoms for instance. When they are very far apart, the force is one of attraction, which varies as the inverse seventh power of the distance, and when they are very close the force is a very large repulsion. If we integrate the inverse seventh power to find the work done, we find that the potential energy U, which is a function of the radial distance between the two oxygen atoms, varies as the inverse sixth power of the distance for large distances.

Fig. 14–3. The potential energy between two atoms as a function of the distance between them.
If we sketch the curve of the potential energy U(r) as in Fig. 14–3, we thus start out at large r with an inverse sixth power, but if we come in sufficiently near, we reach a point d where there is a minimum of potential energy. The minimum of potential energy at r=d means this: if we start at d and move a small distance, a very small distance, the work done, which is the change in potential energy when we move this distance, is nearly zero, because there is very little change in potential energy at the bottom of the curve. Thus, there is no force at this point, and so it is the equilibrium point. Another way to see that it is the equilibrium point is that it takes work to move away from d in either direction. When the two oxygen atoms have settled down, so that no more energy can be liberated from the force between them, they are in the lowest energy state, and they will be at this separation d. This is the way an oxygen molecule looks when it is cold. When we heat it up, the atoms shake and move farther apart, and we can in fact break them apart, but to do so takes a certain amount of work or energy, which is the potential energy difference between r=d and r=∞. When we try to push the atoms very close together the energy goes up very rapidly, because they repel each other.
The reason we bring this out is that the idea of force is not particularly suitable for quantum mechanics; there the idea of energy is most natural. We find that although forces and velocities “dissolve” and disappear when we consider the more advanced forces between nuclear matter and between molecules and so on, the energy concept remains. Therefore, we find curves of potential energy in quantum mechanics books, but very rarely do we ever see a curve for the force between two molecules, because by that time people who are doing analyses are thinking in terms of energy rather than of force.
Next, we note that if several conservative forces are acting on an object at the same time, then the potential energy of the object is the sum of the potential energies from each of the separate forces. This is the same proposition that we mentioned before, because if the force can be represented as a vector sum of forces, then the work done by the total force is the sum of the works done by the partial forces, and it can therefore be analyzed as changes in the potential energies of each of them separately. Thus, the total potential energy is the sum of all the little pieces.
We could generalize this to the case of a system of many objects interacting with one another, like Jupiter, Saturn, Uranus, etc., or oxygen, nitrogen, carbon, etc., which are acting with respect to one another in pairs due to forces all of which are conservative. In these circumstances the kinetic energy in the entire system is simply the sum of the kinetic energies of all of the particular atoms or planets or whatever, and the potential energy of the system is the sum, over the pairs of particles, of the potential energy of mutual interaction of a single pair, as though the others were not there. (This is really not true for molecular forces, and the formula is somewhat more complicated; it certainly is true for Newtonian gravitation, and it is true as an approximation for molecular forces. For molecular forces there is a potential energy, but it is sometimes a more complicated function of the positions of the atoms than simply a sum of terms from pairs.) In the special case of gravity, therefore, the potential energy is the sum, over all the pairs i and j, of −Gmimj/rij, as was indicated in Eq. (13.14). Equation (13.14) expressed mathematically the following proposition: that the total kinetic energy plus the total potential energy does not change with time. As the various planets wheel about, and turn and twist and so on, if we calculate the total kinetic energy and the total potential energy, we find that the total remains constant.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















