The more complicated objects we deal with can be of several kinds: water flowing, galaxies whirling, and so on. The simplest “complicated” object to analyze, at the start, is what we call a rigid body, a solid object that is turning as it moves about. However, even such a simple object may have a most complex motion, and we shall therefore first consider the simplest aspects of such motion, in which an extended body rotates about a fixed axis. A given point on such a body then moves in a plane perpendicular to this axis. Such rotation of a body about a fixed axis is called plane rotation or rotation in two dimensions. We shall later generalize the results to three dimensions, but in doing so we shall find that, unlike the case of ordinary particle mechanics, rotations are subtle and hard to understand unless we first get a solid grounding in two dimensions.

The first interesting theorem concerning the motion of complicated objects can be observed at work if we throw an object made of a lot of blocks and spokes, held together by strings, into the air. Of course, we know it goes in a parabola, because we studied that for a particle. But now our object is not a particle; it wobbles and it jiggles, and so on. It does go in a parabola though; one can see that. What goes in a parabola? Certainly not the point on the corner of the block, because that is jiggling about; neither is it the end of the wooden stick, or the middle of the wooden stick, or the middle of the block. But something goes in a parabola, there is an effective “center” which moves in a parabola. So, our first theorem about complicated objects is to demonstrate that there is a mean position which is mathematically definable, but not necessarily a point of the material itself, which goes in a parabola. That is called the theorem of the center of the mass, and the proof of it is as follows.

We may consider any object as being made of lots of little particles, the atoms, with various forces among them. Let i represent an index which defines one of the particles. (There are millions of them, so i goes to 10²³, or something.) Then the force on the ith particle is, of course, the mass times the acceleration of that particle:

We shall use the nonrelativistic approximation for all quantities. In these circumstances the mass is constant, so that

If we now add the force on all the particles, that is, if we take the sum of all the F_i’s for all the different indexes, we get the total force, F. On the other side of the equation, we get the same thing as though we added before the differentiation:

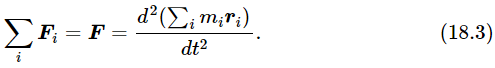
Therefore, the total force is the second derivative of the masses times their positions, added together.

Now the total force on all the particles is the same as the external force. Why? Although there are all kinds of forces on the particles because of the strings, the wigglings, the pulling's and pushing's, and the atomic forces, and who knows what, and we have to add all these together, we are rescued by Newton’s Third Law. Between any two particles the action and reaction are equal, so that when we add all the equations together, if any two particles have forces between them it cancels out in the sum; therefore, the net result is only those forces which arise from other particles which are not included in whatever object we decide to sum over. So, if Eq. (18.3) is the sum over a certain number of the particles, which together are called “the object,” then the external force on the total object is equal to the sum of all the forces on all its constituent particles.

Now it would be nice if we could write Eq. (18.3) as the total mass times some acceleration. We can. Let us say M is the sum of all the masses, i.e., the total mass. Then if we define a certain vector R to be

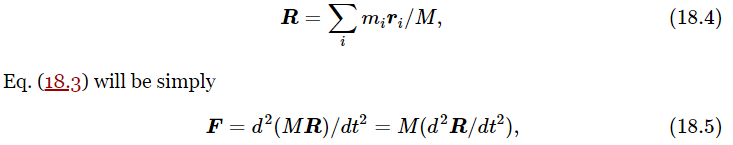
since M is a constant. Thus we find that the external force is the total mass times the acceleration of an imaginary point whose location is R. This point is called the center of mass of the body. It is a point somewhere in the “middle” of the object, a kind of average r in which the different r_i’s have weights or importance's proportional to the masses.

We have remarks from two points: First, if the external forces are zero, if the object were floating in empty space, it might whirl, and jiggle, and twist, and do all kinds of things. But the center of mass, this artificially invented, calculated position, somewhere in the middle, will move with a constant velocity. In particular, if it is initially at rest, it will stay at rest. So, if we have some kind of a box, perhaps a space ship, with people in it, and we calculate the location of the center of mass and find it is standing still, then the center of mass will continue to stand still if no external forces are acting on the box. Of course, the space ship may move a little in space, but that is because the people are walking back and forth inside; when one walks toward the front, the ship goes toward the back so as to keep the average position of all the masses in exactly the same place.

Is it rocket propulsion therefore absolutely impossible because one cannot move the center of mass? No; but of course, we find that to propel an interesting part of the rocket, an uninteresting part must be thrown away. In other words, if we start with a rocket at zero velocity and we spit some gas out the back end, then this little blob of gas goes one way as the rocket ship goes the other, but the center of mass is still exactly where it was before. So, we simply move the part that we are interested in against the part we are not interested in.

The second point concerning the center of mass, which is the reason we introduced it into our discussion at this time, is that it may be treated separately from the “internal” motions of an object, and may therefore be ignored in our discussion of rotation.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل