
Rotational kinetic energy
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 19
الجزء والصفحة:
Volume I, Chapter 19
 2024-03-01
2024-03-01
 1659
1659
In the analogy between linear motion and angular motion, we used the work theorem, but we did not talk about kinetic energy. What is the kinetic energy of a rigid body, rotating about a certain axis with an angular velocity ω? We can immediately guess the correct answer by using our analogies. The moment of inertia corresponds to the mass, angular velocity corresponds to velocity, and so the kinetic energy ought to be 1/2 Iω2, and indeed it is, as will now be demonstrated. Suppose the object is rotating about some axis so that each point has a velocity whose magnitude is ωri, where ri is the radius from the particular point to the axis. Then if mi is the mass of that point, the total kinetic energy of the whole thing is just the sum of the kinetic energies of all of the little pieces:
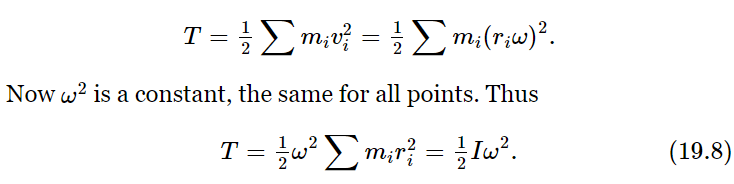
There are some interesting phenomena associated with an object which is not rigid, but which changes from one rigid condition with a definite moment of inertia, to another rigid condition. Namely, in our example of the turntable, we had a certain moment of inertia I1 with our arms stretched out, and a certain angular velocity ω1. When we pulled our arms in, we had a different moment of inertia, I2, and a different angular velocity, ω2, but again we were “rigid.” The angular momentum remained constant, since there was no torque about the vertical axis of the turntable. This means that I1ω1=I2ω2. Now what about the energy? That is an interesting question. With our arms pulled in, we turn faster, but our moment of inertia is less, and it looks as though the energies might be equal. But they are not, because what does balance is Iω, not Iω2. So if we compare the kinetic energy before and after, the kinetic energy before is 12I1ω21=1/2 Lω1, where L= I1ω1= I2ω2 is the angular momentum. Afterward, by the same argument, we have T=1/2 Lω2 and since ω2>ω1 the kinetic energy of rotation is greater than it was before. So, we had a certain energy when our arms were out, and when we pulled them in, we were turning faster and had more kinetic energy. What happened to the theorem of the conservation of energy? Somebody must have done some work. We did work! When did we do any work? When we move a weight horizontally, we do not do any work. If we hold a thing out and pull it in, we do not do any work. But that is when we are not rotating! When we are rotating, there is centrifugal force on the weights. They are trying to fly out, so when we are going around, we have to pull the weights in against the centrifugal force. So, the work we do against the centrifugal force ought to agree with the difference in rotational energy, and of course it does. That is where the extra kinetic energy comes from.
There is still another interesting feature which we can treat only descriptively, as a matter of general interest. This feature is a little more advanced, but is worth pointing out because it is quite curious and produces many interesting effects.
Consider that turntable experiment again. Consider the body and the arms separately, from the point of view of the man who is rotating. After the weights are pulled in, the whole object is spinning faster, but observe, the central part of the body is not changed, yet it is turning faster after the event than before. So, if we were to draw a circle around the inner body, and consider only objects inside the circle, their angular momentum would change; they are going faster. Therefore, there must be a torque exerted on the body while we pull in our arms. No torque can be exerted by the centrifugal force, because that is radial. So that means that among the forces that are developed in a rotating system, centrifugal force is not the entire story, there is another force. This other force is called Coriolis force, and it has the very strange property that when we move something in a rotating system, it seems to be pushed sidewise. Like the centrifugal force, it is an apparent force. But if we live in a system that is rotating, and move something radially, we find that we must also push it sidewise to move it radially. This sidewise push which we have to exert is what turned our body around.
Now let us develop a formula to show how this Coriolis force really works. Suppose Moe is sitting on a carousel that appears to him to be stationary. But from the point of view of Joe, who is standing on the ground and who knows the right laws of mechanics, the carousel is going around. Suppose that we have drawn a radial line on the carousel, and that Moe is moving some mass radially along this line. We would like to demonstrate that a sidewise force is required to do that. We can do this by paying attention to the angular momentum of the mass. It is always going around with the same angular velocity ω, so that the angular momentum is
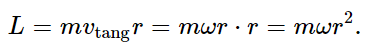
So when the mass is close to the center, it has relatively little angular momentum, but if we move it to a new position farther out, if we increase r, m has more angular momentum, so a torque must be exerted in order to move it along the radius. (To walk along the radius in a carousel, one has to lean over and push sidewise. Try it sometime.) The torque that is required is the rate of change of L with time as m moves along the radius. If m moves only along the radius, omega stays constant, so that the torque is

where Fc is the Coriolis force. What we really want to know is what sidewise force has to be exerted by Moe in order to move m out at speed vr=dr/dt. This is Fc= τ/r= 2mωvr.
Now that we have a formula for the Coriolis force, let us look at the situation a little more carefully, to see whether we can understand the origin of this force from a more elementary point of view. We note that the Coriolis force is the same at every radius, and is evidently present even at the origin! But it is especially easy to understand it at the origin, just by looking at what happens from the inertial system of Joe, who is standing on the ground. Figure 19–4 shows three successive views of m just as it passes the origin at t=0. Because of the rotation of the carousel, we see that m does not move in a straight line, but in a curved path tangent to a diameter of the carousel where r=0. In order for m to go in a curve, there must be a force to accelerate it in absolute space. This is the Coriolis force.
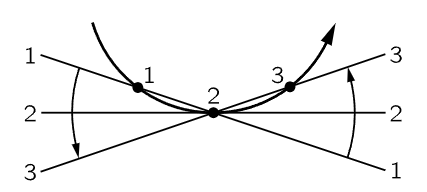
Fig. 19–4. Three successive views of a point moving radially on a rotating turntable.
This is not the only case in which the Coriolis force occurs. We can also show that if an object is moving with constant speed around the circumference of a circle, there is also a Coriolis force. Why? Moe sees a velocity vM around the circle. On the other hand, Joe sees m going around the circle with the velocity vJ=vM+ωr, because m is also carried by the carousel. Therefore, we know what the force really is, namely, the total centripetal force due to the velocity vJ, or mv2J/r; that is the actual force. Now from Moe’s point of view, this centripetal force has three pieces. We may write it all out as follows:
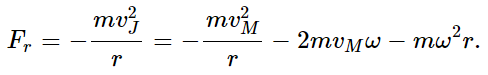
Now, Fr is the force that Moe would see. Let us try to understand it. Would Moe appreciate the first term? “Yes,” he would say, “even if I were not turning, there would be a centripetal force if I were to run around a circle with velocity vM.” This is simply the centripetal force that Moe would expect, having nothing to do with rotation. In addition, Moe is quite aware that there is another centripetal force that would act even on objects which are standing still on his carousel. This is the third term. But there is another term in addition to these, namely the second term, which is again 2mωv. The Coriolis force Fc was tangential when the velocity was radial, and now it is radial when the velocity is tangential. In fact, one expression has a minus sign relative to the other. The force is always in the same direction, relative to the velocity, no matter in which direction the velocity is. The force is at right angles to the velocity, and of magnitude 2mωv.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


