
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Analogs in physics
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 25
2024-03-14
1937
The next aspect of this review is to note that masses and springs are not the only linear systems; there are others. In particular, there are electrical systems called linear circuits, in which we find a complete analog to mechanical systems. We did not learn exactly why each of the objects in an electrical circuit works in the way it does—that is not to be understood at the present moment; we may assert it as an experimentally verifiable fact that they behave as stated.
For example, let us take the simplest possible circumstance. We have a piece of wire, which is just a resistance, and we have applied to it a difference in potential, V. Now the V means this: if we carry a charge q through the wire from one terminal to another terminal, the work done is qV. The higher the voltage difference, the more work was done when the charge, as we say, “falls” from the high potential end of the terminal to the low potential end. So charges release energy in going from one end to the other. Now the charges do not simply fly from one end straight to the other end; the atoms in the wire offer some resistance to the current, and this resistance obeys the following law for almost all ordinary substances: if there is a current I, that is, so and so many charges per second tumbling down, the number per second that comes tumbling through the wire is proportional to how hard we push them—in other words, proportional to how much voltage there is:
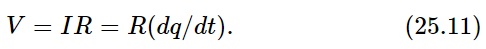
The coefficient R is called the resistance, and the equation is called Ohm’s Law. The unit of resistance is the ohm; it is equal to one volt per ampere. In mechanical situations, to get such a frictional force in proportion to the velocity is difficult; in an electrical system it is very easy, and this law is extremely accurate for most metals.
We are often interested in how much work is done per second, the power loss, or the energy liberated by the charges as they tumble down the wire. When we carry a charge q through a voltage V, the work is qV, so the work done per second would be V(dq/dt), which is the same as VI, or also IR⋅I=I2R. This is called the heating loss—this is how much heat is generated in the resistance per second, by the conservation of energy. It is this heat that makes an ordinary incandescent light bulb work.
Of course, there are other interesting properties of mechanical systems, such as the mass (inertia), and it turns out that there is an electrical analog to inertia also. It is possible to make something called an inductor, having a property called inductance, such that a current, once started through the inductance, does not want to stop. It requires a voltage in order to change the current! If the current is constant, there is no voltage across an inductance. dc circuits do not know anything about inductance; it is only when we change the current that the effects of inductance show up. The equation is

and the unit of inductance, called the henry, is such that one volt applied to an inductance of one henry produces a change of one ampere per second in the current. Equation (25.12) is the analog of Newton’s law for electricity, if we wish: V corresponds to F, L corresponds to m, and I corresponds to velocity! All of the consequent equations for the two kinds of systems will have the same derivations because, in all the equations, we can change any letter to its corresponding analog letter and we get the same equation; everything we deduce will have a correspondence in the two systems.
Now what electrical thing corresponds to the mechanical spring, in which there was a force proportional to the stretch? If we start with F=kx and replace F→V and x→q, we get V=αq. It turns out that there is such a thing, in fact it is the only one of the three circuit elements we can really understand, because we did study a pair of parallel plates, and we found that if there were a charge of certain equal, opposite amounts on each plate, the electric field between them would be proportional to the size of the charge. So the work done in moving a unit charge across the gap from one plate to the other is precisely proportional to the charge. This work is the definition of the voltage difference, and it is the line integral of the electric field from one plate to another. It turns out, for historical reasons, that the constant of proportionality is not called C, but 1/C. It could have been called C, but it was not. So we have

The unit of capacitance, C, is the farad; a charge of one coulomb on each plate of a one-farad capacitor yields a voltage difference of one volt.
There are our analogies, and the equation corresponding to the oscillating circuit becomes the following, by direct substitution of L for m, q for x, etc:
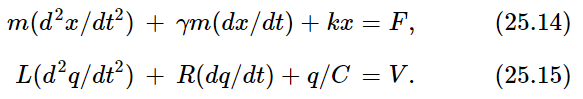
Now everything we learned about (25.14) can be transformed to apply to (25.15). Every consequence is the same; so much the same that there is a brilliant thing we can do.
Suppose we have a mechanical system which is quite complicated, not just one mass on a spring, but several masses on several springs, all hooked together. What do we do? Solve it? Perhaps; but look, we can make an electrical circuit which will have the same equations as the thing we are trying to analyze! For instance, if we wanted to analyze a mass on a spring, why can we not build an electrical circuit in which we use an inductance proportional to the mass, a resistance proportional to the corresponding mγ, 1/C proportional to k, all in the same ratio? Then, of course, this electrical circuit will be the exact analog of our mechanical one, in the sense that whatever q does, in response to V (V also is made to correspond to the forces that are acting), so the x would do in response to the force! So if we have a complicated thing with a whole lot of interconnecting elements, we can interconnect a whole lot of resistances, inductances, and capacitances, to imitate the mechanically complicated system. What is the advantage to that? One problem is just as hard (or as easy) as the other, because they are exactly equivalent. The advantage is not that it is any easier to solve the mathematical equations after we discover that we have an electrical circuit (although that is the method used by electrical engineers!), but instead, the real reason for looking at the analog is that it is easier to make the electrical circuit, and to change something in the system.
Suppose we have designed an automobile, and want to know how much it is going to shake when it goes over a certain kind of bumpy road. We build an electrical circuit with inductances to represent the inertia of the wheels, spring constants as capacitances to represent the springs of the wheels, and resistors to represent the shock absorbers, and so on for the other parts of the automobile. Then we need a bumpy road. All right, we apply a voltage from a generator, which represents such and such a kind of bump, and then look at how the left wheel jiggles by measuring the charge on some capacitor. Having measured it (it is easy to do), we find that it is bumping too much. Do we need more shock absorber, or less shock absorber? With a complicated thing like an automobile, do we actually change the shock absorber, and solve it all over again? No!, we simply turn a dial; dial number ten is shock absorber number three, so we put in more shock absorber. The bumps are worse—all right, we try less. The bumps are still worse; we change the stiffness of the spring (dial 17), and we adjust all these things electrically, with merely the turn of a knob.
This is called an analog computer. It is a device which imitates the problem that we want to solve by making another problem, which has the same equation, but in another circumstance of nature, and which is easier to build, to measure, to adjust, and to destroy!
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















