
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Polar and axial vectors
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 52
2024-07-15
2101
Now we go further. We observe that in physics there are a lot of other places where we have “right” and “left” hand rules. As a matter of fact, when we learned about vector analysis, we learned about the right-hand rules we have to use in order to get the angular momentum, torque, magnetic field, and so on, to come out right. The force on a charge moving in a magnetic field, for example, is F=qv×B. In a given situation, in which we know F, v, and B, isn’t that equation enough to define right-handedness? As a matter of fact, if we go back and look at where the vectors came from, we know that the “right-hand rule” was merely a convention; it was a trick. The original quantities, like the angular momenta and the angular velocities, and things of this kind, were not really vectors at all! They are all somehow associated with a certain plane, and it is just because there are three dimensions in space that we can associate the quantity with a direction perpendicular to that plane. Of the two possible directions, we chose the “right-hand” direction.
So if the laws of physics are symmetrical, we should find that if some demon were to sneak into all the physics laboratories and replace the word “right” for “left” in every book in which “right-hand rules” are given, and instead we were to use all “left-hand rules,” uniformly, then it should make no difference whatever in the physical laws.
Let us give an illustration. There are two kinds of vectors. There are “honest” vectors, for example a step r in space. If in our apparatus there is a piece here and something else there, then in a mirror apparatus there will be the image piece and the image something else, and if we draw a vector from the “piece” to the “something else,” one vector is the mirror image of the other (Fig. 52–2). The vector arrow changes its head, just as the whole space turns inside out; such a vector we call a polar vector.

Fig. 52–2.A step in space and its mirror image.
But the other kind of vector, which has to do with rotations, is of a different nature. For example, suppose that in three dimensions something is rotating as shown in Fig. 52–3. Then if we look at it in a mirror, it will be rotating as indicated, namely, as the mirror image of the original rotation. Now we have agreed to represent the mirror rotation by the same rule, it is a “vector” which, on reflection, does not change about as the polar vector does, but is reversed relative to the polar vectors and to the geometry of the space; such a vector is called an axial vector.
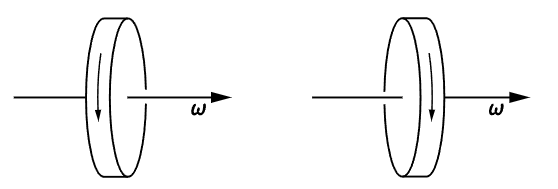
Fig. 52–3.A rotating wheel and its mirror image. Note that the angular velocity “vector” is not reversed in direction.
Now if the law of reflection symmetry is right in physics, then it must be true that the equations must be so designed that if we change the sign of each axial vector and each cross-product of vectors, which would be what corresponds to reflection, nothing will happen. For instance, when we write a formula which says that the angular momentum is L=r×p, that equation is all right, because if we change to a left-hand coordinate system, we change the sign of L, but p and r do not change; the cross-product sign is changed, since we must change from a right-hand rule to a left-hand rule. As another example, we know that the force on a charge moving in a magnetic field is F=qv×B, but if we change from a right- to a left-handed system, since F and v are known to be polar vectors the sign change required by the cross-product must be cancelled by a sign change in B, which means that B must be an axial vector. In other words, if we make such a reflection, B must go to −B. So if we change our coordinates from right to left, we must also change the poles of magnets from north to south.
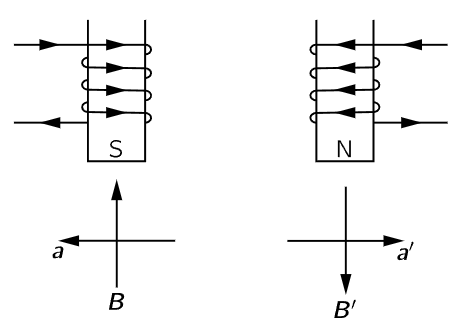
Fig. 52–4. A magnet and its mirror image.
Let us see how that works in an example. Suppose that we have two magnets, as in Fig. 52–4. One is a magnet with the coils going around a certain way, and with current in a given direction. The other magnet looks like the reflection of the first magnet in a mirror—the coil will wind the other way, everything that happens inside the coil is exactly reversed, and the current goes as shown. Now, from the laws for the production of magnetic fields, which we do not know yet officially, but which we most likely learned in high school, it turns out that the magnetic field is as shown in the figure. In one case the pole is a south magnetic pole, while in the other magnet the current is going the other way and the magnetic field is reversed—it is a north magnetic pole. So, we see that when we go from right to left, we must indeed change from north to south!
Never mind changing north to south; these too are mere conventions. Let us talk about phenomena. Suppose, now, that we have an electron moving through one field, going into the page. Then, if we use the formula for the force, v×B (remember the charge is minus), we find that the electron will deviate in the indicated direction according to the physical law. So, the phenomenon is that we have a coil with a current going in a specified sense and an electron curves in a certain way—that is the physics—never mind how we label everything.
Now let us do the same experiment with a mirror: we send an electron through in a corresponding direction and now the force is reversed, if we calculate it from the same rule, and that is very good because the corresponding motions are then mirror images!
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















