
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
جمع المتجهات Addition of Vectors
المؤلف:
محمد عطية سويلم، د. محمد روبين إدريس، بديع صالح الخطيب، د. أحمد يوسف قواسمة
المصدر:
الفيزياء العامة
الجزء والصفحة:
ص 30
9-8-2017
58832
جمع المتجهات Addition of Vectors
لفهم القاعدة في جمع المتجهات ، فإننا سنأخذ حالة الإزاحة . ففي الشكل (1) ، اذا تحركت الدقيقة المادية من أ إلى ب فإن ازاحتها هي r1 واذا تحركت إلى ج بإزاحة r2 فإن الإزاحة الكلية هي :
(1-1) ………….. r = r1 + r2
ونلاحظ هنا أن الإزاحة الكلية هذه مساوية لإزاحة الدقيقة فيما لو تحركت من أ إلى ج مباشرة . صحيح أن المسافة المقطوعة في الحالتين مختلفة ، إلا أن النتيجة الكلية واحدة وهي r .

الشكل (1)
والجمع في المعادلة (1-1) هو جمع اتجاهي . ويجب أن لا يخلط بينه وبين الجمع العددي r = r1 + r2 ، فهنا يجوز تعويض قيم كل من r2 ، r1 مباشرة ؛ أما في الجمع الاتجاهي في المعادلة (1-1) ، فلا يجوز تعويض المقادير مباشرة ؛ فمثلا لدينا المتجهات الثلاثة C , B , A حيث C = A + B
5 = |A| وحدات ، 6 = |B| وحدات . هنا لا يجوز أن نقول |C| = 5+6 = 11 ، بل نجد مقدار المتجه C بإحدى طريقتين ، هما : طريقة الرسم ، وطريقة الحساب .
1-1 طريقة الرسم :
تتم طريقة الرسم هذه باسم يتم اختيار مقياس رسم مناسب . ثم نرسم احد المتجهات المراد جمعها مقداراً واتجاها . من نهاية هذا المتجه نرسم موازيا للمتجه الثاني ويمثله مقدارا واتجاها ، من نهاية المتجه الثاني ، نرسم موازيا للمتجه الثالث ويمثله مقداراً واتجاها ، ومن نهاية المتجه الثاني ، نرسم موازيا للمتجه الثالث ومثله مقدارا واتجاها ، وهكذا حتى نهاية المتجهات جميعها . فمثلا لو أردنا جمع المتجهات : D, C, B, A في الشكل (2- أ) ، نجد أن المحصلة كما هي مبينة في الرسم (2- ب) هي R . ولإيجاد مقدار R ، نقيسها بالمسطرة ، ونضرب في مقياس الرسم . أما اتجاه R ، فنجده من قياس الزاوية (a) التي يصنعها حاصل الجمع مع المتجه A ، حيث :
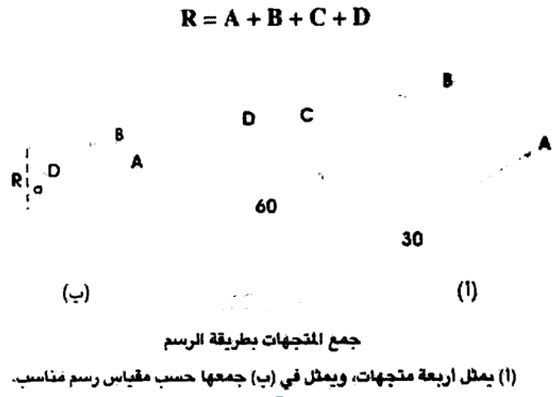
الشكل (2)
إذا كان المراد هو إيجاد مجموع متجهين ، فإن الشكل المغلق الذي نحصل عليه هو مثلث ، أما إذا كان المطلوب هو إيجاد ناتج جمع أكثر من متجهين ، فإن الشكل المغلق المتكون هو مضلع يسمى بمضلع القوى . وسواء كان الشكل مثلثاً أم مضلعاً ، فإن ناتج الجمع المحصلة يكون اتجاهه بعكس الاتجاه الدوراني لأسهم المتجهات المكونة للمضلع . فإذا كان الاتجاه الدوراني لأسهم المتجهات هو عكس عقارب الساعة ، فإن اتجاه المحصلة يكون باتجاه عقارب الساعة . وتسمى طريقة الرسم هذه أيضاً طريقة الرسم من الرأس إلى الذيل ، لأن ذيل المتجه يلتقي مع رأس المتجه الذي يسبقه .... وهكذا .

الشكل (3)
1-2 طريقة الحساب (طريقة متوازي الاضلاع) :
تعد هذه الطريقة الحسابية طريقة سهلة في إيجاد مقدار واتجاه محصلة ، أو ناتج جمع متجهين بينهما زاوية ، فإذا رسمنا المتجهين B,A من النقطة " O " نفسها وكانت الزاوية بينهما 0 ثم أكملنا متوازي الاضلاع الذي يكون فيه المتجهان B , A ضلعين متجاورين ، فإن قطر متوازي الاضلاع '' OP ''الذي يتحد مع المتجهين في نقطة البداية يكون هو ناتج جمع المتجهين B , A مقدارا واتجاها ، كما في الشكل (4) .

الشكل (4)
وليس شرطا هنا أن يتم الرسم بمقياس رسم ، أو أن يكون دقيقاً تماما ، لأن الرسم هو فقط لبيان موقع المحصلة أو ناتج الجمع من المتجهين : أما مقدار المحصلة واتجاهها ، فيتم ايجادهما بطريقة حسابية كما يأتي :
أ- حساب مقدار حاصل الجمع R = A + B
لحساب مقدار R فإننا نستخدم قانون جيب التمام الذي يعطى بالعلاقة :
(1)......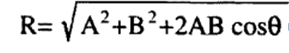
حيث θهي الزاوية المحصورة بين المتجهين A , B
ب- ايجاد اتجاه المحصلة R .
لا يجاد الاتجاه فإننا نجد الزاوية المحصورة بين المحصلة R وبين أي من المتجهين A أو B فإذا فرضنا أن الزاوية بين A , R هي a ، فإننا نجد مقدار الزاوية a من قانون الجيب الذي ينص على أنه : في أي مثلث ، ناتج قسمة طول الضلع على جيب الزاوية المقابلة له يساوي ناتج قسمة الضلع الآخر على جيب الزاوية المقابلة له . وعليه فإن المعادلة حسب القانون هي :
(2)......
ومنه ، فإن الزاوية (a) تساوي :
(3)........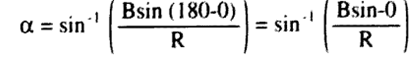
أي أن (a) هي الزاوية التي جيبها المقدار داخل القوس ، علما بأن :
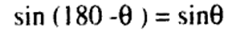
وفي حالة الخاصة التي يكون فيها المتجهان متعامدين ، أي 90° = 0 ، فإن العلاقتين السابقتين تصبحان :
(4).........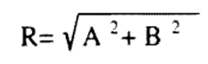
(5)........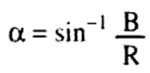
حيث (a) هي الزاوية بين المحصلة R والمتجه A .
والجدير بالذكر أنه يمكن استخدام طريقة متوازي الأضلاع لحساب مجموع ثلاثة متجهات أو اكثر ، وذلك بإيجاد محصلة متجهين أولا ، وبعد معرفة الزوايا ، نجد محصلة هذه المحصلة والمتجه الثالث ، وهكذا إلا أن هذه الطريقة طويلة وغير عملية ، ويستعاض عنها بطريقة التحليل التي سنبحثها في بند لاحق . ويمكن الاستنتاج من طريقة متوازي الأضلاع أن عملية جمع المتجهات عملية قابلة للتبديل '' commutaive " أي أن :
(6) ……………. A + B = B + A
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















