ضرب المتجهات Vector Product

عند ضرب متجه مثل (A) في عدد معين ، فانه ينتج لدينا متجه جديد له اتجاه (A) ومقداره يساوي مقدار (A) مضروبا في العدد , فمثلا المتجه :

(1)…………………..      B=5 A       

يعني هذا أن المتجه B يكون في اتجاه (A) ، لكن مقداره يساوي خمسة أمثال مقدار (A) بالإضافة إلى هذا النوع من الضرب ، فإن هناك نوعين آخرين من الضرب لهما فائدة كبيرة ، واستخدامات جمة في علم الفيزياء والميكانيك والكهرباء وغيرها . وهما ، الضرب العددي Scalar))  والضرب الاتجاهي Vector)) ونعرض في ما يأتي شرحا لكل منهما :

1-1 الضرب العددي : Scalar Product

ويقال له أحيانا الضرب القياسي أو النقطي (Dot Product) أو الداخلي (Inner Product) . لكن جميعها تشير إلى شيء واحد ، وهو أن ضرب أي متجهين ضربا عدديا يعطينا في النتيجة كمية عددية ليس لها اتجاه . فمثلا ضرب القوة (كمية متجهة) في الإزاحة (كمية متجهة) يعطينا الشغل ، وهو كمية عددية , إذن نضرب القوة في الإزاحة ضربا نقطياً ليعطينا الشغل .

الضرب العددي بين متجهين يعني ضرب مقدار أحدهما في المسقط العمودي للمتجه الآخر عليه .

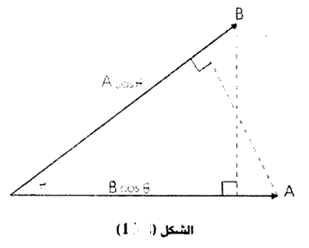
ويميز الضرب القياسي بوضع نقطة بين المتجهين المضروبين ، مثل B ، A وتلفظ (A dot B) أو (B نقطة A) ، وأحيانا تلفظ (A) تداخل (B) , ولإيجاد ناتج الضرب ، فإننا نضرب مقدار المتجه الأول في مقدار المتجه الثاني في جيب تمام الزاوية بينهما (الزاوية الصغرى بينهما) ، وذلك حسب العلاقة :

(2) ……………             R= A.B = ABcos0

والشكل (1) يوضح معنى الضرب الداخلي (العددي) ، حيث يبين ان (Acosθ) هي المسقط العمودي للمتجه (A) على اتجاه المتجه (B) ، وأن (Acosθ) هي المسقط العمودي للمتجه (B) على اتجاه المتجه (A) . وهذا يعني أن الضرب العددي للمتجهين يعني مقدار أحدهما مضروبا في مسقط الآخر عليه .

فإذا كان المتجهان متعامدين ، فإن cos 90° = zero وعليه فإن :

A.B = zero (لان A ⊥ B)

وهو شرط تعامد أي متجهين .

وفي حالة توازي المتجهين ، فإن = 1° θ​ Cosوعليه ، فإن :

A.B = AB (لأن B//A)

ومن تعريف الضرب العددي يتبين لنا ان هذا النوع من الضرب قابل للتبديل ، أي أن :

(3)………..        A . B = B.A

وذلك لان النتيجة في الحالتين هي عددية ليس لها اتجاه . وكذلك من السهل علينا أن نتبين من خلال الربط بين مفهوم المسقط العمودي والضرب العددي أن هذا الضرب هو أيضا قابل للتوزيع على الجمع ، أي أن :

(4) …………. A. (B+C) = A.B+A.C

وباستخدام هذه القابلية ، وتعريف الضرب العددي ، يمكن إثبات قانون جيب التمام  .

 1-2 الضرب الاتجاهي  Vector Product

ويسمى أيضا بالضرب التقاطعي Cross product ، ويكتب بوضع إشارة " x " بين المتجهين مثل A × B وتلفظ A تقاطع B ويختلف الضرب الاتجاهي عن الضرب القياسي في أن حاصل الضرب يكون متجها جديدا ، كما هو واضح من التسمية ، إذن :

A × B = R             .................. (5)

لاحظ هنا أن R هي كمية متجهة ، لكن R في الضرب العددي (المعادلة 1) هي كمية عددية . ولذلك عندما يطلب إلينا إيجاد حاصل الضرب التقاطعي لمتجهين ، وجب علينا إيجاد قيمة (مقدار حاصل الضرب ، ومن ثم تعيين اتجاه المتجه الذي يمثل حاصل الضرب التقاطعي للمتجهين . ونجد مقدار المتجه (R) بالعلاقة :

(6) ………………             R= AB sin 0

حيث (0) هي الزاوية الصغرى المحصورة بين المتجهين A ، B أما اتجاه R فيكون دائما متعامدا مع كل من المتجهين A ، B عند نقطة التقائهما ، أو بعبارة أخرى عمودياً على المستوى الذي يجمع المتجهين . ويكون اتجاهه باتجاه حركة البرغي عندما يتم إدارته من A إلى B عبر الزاوية الصغرى بينهما . أو يمكن إيجاد اتجاهه بتطبيق قاعدة قبضة اليد اليمنى : إذ تحرك الأصابع الأربعة للكف اليمنى باتجاه من A إلى B عبر الزاوية الصغرى ، فيكون اتجاه A × B حسب الاتجاه الذي يشير إليه الإبهام ، كما في الشكل (2) .

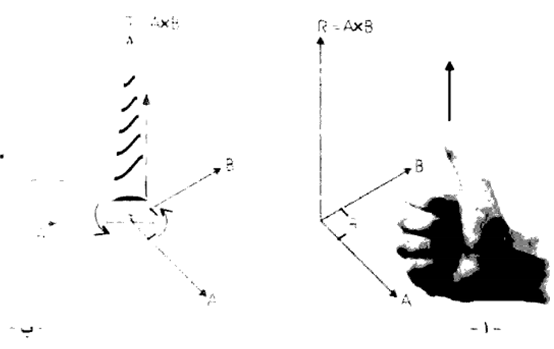
الشكل (2)

أ- التمثيل الهندسي للضرب الاتجاهي . وناتج ضرب أي متجهين يكون متجها اتجاهه يحدد بقاعدة قبضة اليد اليمنى أو باتجاه حركة البرغي .

ب- مقدار ناتج الضرب الاتجاهي لمتجهين يساوي مساحة متوازي الأضلاع المكون منهما .

ويظهر من الشكل (2- ب) أن مقدار ناتج الضرب التقاطعي للمتجهين B , A يساوي مساحة متوازي الأضلاع المكون منهما ؛ لأن :

Bsin0)) A = B × A (من حيث المقدار)

حيث (A) تمثل قاعدة متوازي الأضلاع و Bsin0)) تمثل ارتفاع متوازي الأضلاع .

ولما كان اتجاه حاصل الضرب التقاطعي يحدد بقاعدة البرغي ، إذن يتضح لنا أن تبديل موقعي المتجهين يعكس إشارة أو اتجاه حاصل الضرب التقاطعي : أي أن :

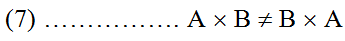
والعلاقة الصحيحة بينهما هي :

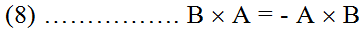
ولذلك فإن الضرب الاتجاهي غير قابل للتبديل " Anticommutative " وبالنظر إلى العلاقة بين الضرب الاتجاهي لمتجهين ومساحة ومتوازي الأضلاع المكون منهما ؛ فإنه يمكن إثبات أن الضرب الاتجاهي قابل للتوزيع  " Destributive Over Addition "

واذا كان المتجهان A,B متوازيين ، فإن الزاوية بينهما تساوي صفرا ، وجيب الزاوية صفر يساوي صفرا ، إذن في حالة التوازي يكون

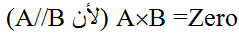
ولذلك فإن شرط توازي متجهين هو أن يكون ناتج الضرب الاتجاهي لهما يساوي صفرا .

مواضيع ذات صلة

أصول عدم الانعكاس

الانعكاس يولد الانعكاس

الاحتمالية في الميكانيكا الإحصائية

القابلية للانعكاس وعدم القابلية للانعكاس

نظرة في تعددية الفيزياء

الاختزال وعدم القابلية للانعكاس

الواقعية العلمية وتغيير النظريات

نقص الإثبات ومذهب الذرائعية ومذهب الواقعية

مشكلة التمييز: متى يكون المنهج علميا؟

المنهج العلمي: من الاستقراء إلى التكذيب وما بعده

مناهج العلوم وثمارها

!Parity is not conserved