تحليل المتجهات Vector Analysis

إما أن يكون المتجه في بعد واحد ، كالاتجاه السيني ، أو الصادي ، أو في بعدين ، أي في كلا الاتجاهين ، أوفي ثلاثة أبعاد أو أكثر . ومهما كانت الحالة ، فإنه يمكننا اعتبار أن أي متجه عبارة عن مجموع متجهين أو أكثر . ومجموعة المتجهات التي تجمع لتكون متجها واحدا تسمى مركبات (Components) هذا المتجه.

تسمى عطية جمع متجهين أو أكثر لإعطاء متجه واحد عملية تركيب المتجهات . أما في حالة الاستعاضة عن المتجه بمتجهين أو أكثر ، فإن العملية تسمى تحليل المتجهات . وأسهل الطرق وأكثرها شيوعا في تحليل المتجهات هي استخدام المحاور المتعامدة .

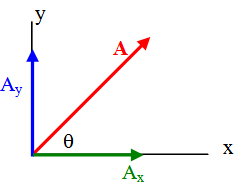
الشكل (1): تحليل المتجه (A) الى مركبتين (A_x)  و(A_y)

ففي حالة تحليل المتجه A في البعدين المتعامدين  X , Y ، فإن المتجه A يساوي مجموع متجهين متعامدين يتحدان معه في نقطة البداية ، وأحدهما يكون في الاتجاه السيني ، والآخر يكون في الاتجاه الصادي . بحيث يكون المتجه A هو قطر متوازي الأضلاع المكون من المتجهين (المركبتين) , والشكل (13-2) يبين مركبتي المتجه A .

حيث

المركبة السينية            (1) ………………………..  A_x = Acos 0

والمركبة الصادية                          (2) ………………Ay = Asin 0

علمأ بان المتجه (A) هو حاصل جمع المتجهين A_x . Ay

(3) ………………… A= A_x + A_y

ومركبة المتجه في اتجاه ما تعني المسقط العمودي لهذا المتجه على هذا الاتجاه . ولايجاد ذلك ، نسقط عمودا من رأس المتجه ٨ على الاتجاه السيني ، فتكون المركبة في هذا

الاتجاه ٨٢ هي المتجه الواصل من نقطة الأصل الى رأس القائمة (نقطة إسقاط العمود). وبتطبيق نظرية فيثاغورس ، فان :

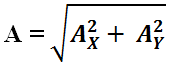  ..................................... (4)

إن عملية تحليل المتجهات تفيد في جمع ثلاثة متجهات أو أكثر .

مواضيع ذات صلة

أصول عدم الانعكاس

الانعكاس يولد الانعكاس

الاحتمالية في الميكانيكا الإحصائية

القابلية للانعكاس وعدم القابلية للانعكاس

نظرة في تعددية الفيزياء

الاختزال وعدم القابلية للانعكاس

الواقعية العلمية وتغيير النظريات

نقص الإثبات ومذهب الذرائعية ومذهب الواقعية

مشكلة التمييز: متى يكون المنهج علميا؟

المنهج العلمي: من الاستقراء إلى التكذيب وما بعده

مناهج العلوم وثمارها

!Parity is not conserved