Simple Harmonic Motion
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 176
30-12-2016
4204
Simple Harmonic Motion
An important property of oscillatory motion is the frequency f which is the number of oscillations completed each second. The units are sec-1 or Hertz, often abbreviated as Hz. Thus
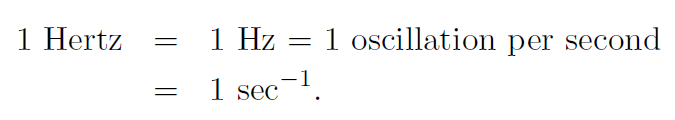
Another related quantity is the period T which is the time taken to complete 1 full oscillation. Now
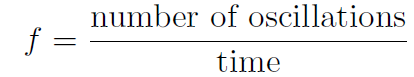
and if the time is simply T then 1 oscillation is completed. Thus
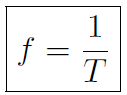
In circular motion, which is a type of oscillatory motion, we introduced the angular speed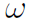 
defined as
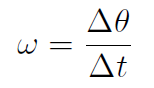
Clearly if Δθ = 2π then Δt = T giving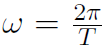 
. Thus angular velocity and frequency are related by
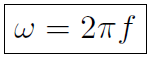
In oscillations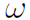 
is often called angular frequency. Any motion that repeats itself at regular intevals is called oscillatory motion or harmonic motion. Now of all the mathematical functions that you have ever come across, there is one famous function that displays oscillations and that is cos θ, which is plotted in Figure 1.1.
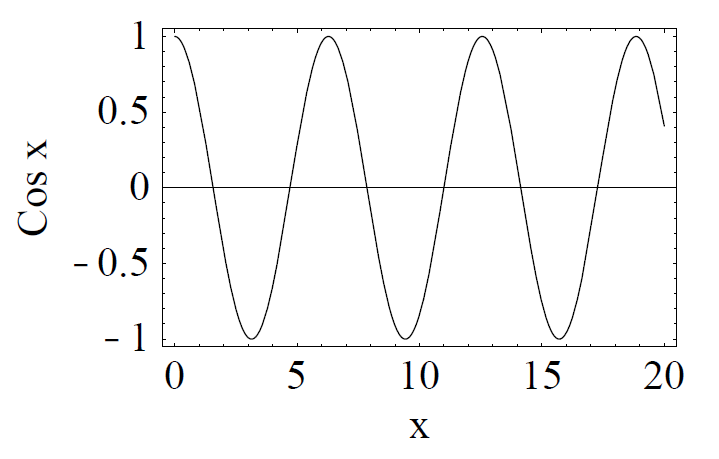
FIGURE 1.1 Plot of cos θ.
Thus the displacement x for oscillatory motion can be written
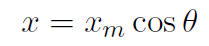
but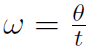 
, giving
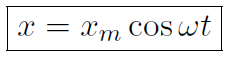
We can also introduce a phase angle ϕ if we want and instead write
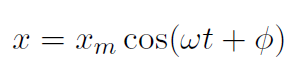
Here xm refers to the maximum value of the displacement x. And xm is often called the amplitude of the motion. Any motion that obeys the above equation x = xm cos !t is called Simple Harmonic Motion (SHM). The velocity of SHM is easy to figure out. First recall that if y = cos kx then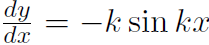 
. Now the velocity is
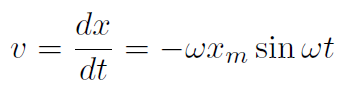
Also recall if y = sin kx when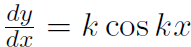 
. Now the acceleration is
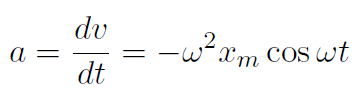
from which it follows that
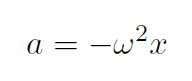
Notice that when x and a are at a maximum, then v is a minimum and vice-versa.
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
