


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2020
Date: 8-12-2020
Date: 8-7-2020
|
The smallest nontrivial taxicab number, i.e., the smallest number representable in two ways as a sum of two cubes. It is given by
 |
The number derives its name from the following story G. H. Hardy told about Ramanujan. "Once, in the taxi from London, Hardy noticed its number, 1729. He must have thought about it a little because he entered the room where Ramanujan lay in bed and, with scarcely a hello, blurted out his disappointment with it. It was, he declared, 'rather a dull number,' adding that he hoped that wasn't a bad omen. 'No, Hardy,' said Ramanujan, 'it is a very interesting number. It is the smallest number expressible as the sum of two [positive] cubes in two different ways' " (Hofstadter 1989; Kanigel 1991; Snow 1993; Hardy 1999, pp. 13 and 68).
This property of 1729 was mentioned by the character Robert the sometimes insane mathematician, played by Anthony Hopkins, in the 2005 film Proof. It was also part of the designation of the spaceship Nimbus BP-1729 appearing in Season 2 of the animated television series Futurama episode DVD 2ACV02 (Greenwald; left figure), as well as the robot character Bender's serial number, as portrayed in a Christmas card in the episode Xmas Story (Volume 2 DVD, Georgoulias et al. 2004; right figure).
REFERENCES:
Georgoulias, T.; Greenwald, S. J.; and Wichterich, M. "Futurama 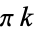 : Mathematics in the Year 3000." Math Horizons, 12-15, Apr. 2004.
: Mathematics in the Year 3000." Math Horizons, 12-15, Apr. 2004.
Greenwald, S. "Dr. Sarah's Futurama 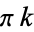 --Mathematics in the Year 3000." https://www.mathsci.appstate.edu/~sjg/futurama/.
--Mathematics in the Year 3000." https://www.mathsci.appstate.edu/~sjg/futurama/.
Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 564, 1989.
Kanigel, R. The Man Who Knew Infinity: A Life of the Genius Ramanujan. New York: Washington Square Press, p. 312, 1991.
Snow, C. P. Foreword to Hardy, G. H. A Mathematician's Apology, reprinted with a foreword by C. P. Snow. New York: Cambridge University Press, p. 37, 1993.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|