
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-12-2019
Date: 12-2-2020
Date: 23-12-2019
|
To define a recurring digital invariant of order 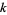 , compute the sum of the
, compute the sum of the 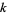 th powers of the digits of a number
th powers of the digits of a number 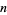 . If this number
. If this number 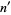 is equal to the original number
is equal to the original number 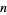 , then
, then 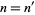 is called a
is called a 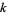 -Narcissistic number. If not, compute the sums of the
-Narcissistic number. If not, compute the sums of the 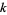 th powers of the digits of
th powers of the digits of 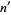 , and so on. If this process eventually leads back to the original number
, and so on. If this process eventually leads back to the original number 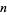 , the smallest number in the sequence
, the smallest number in the sequence 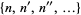 is said to be a
is said to be a 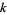 -recurring digital invariant. For example,
-recurring digital invariant. For example,
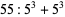 |
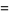 |
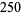 |
(1) |
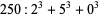 |
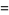 |
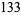 |
(2) |
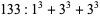 |
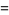 |
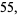 |
(3) |
so 55 is an order 3 recurring digital invariant. The following table gives recurring digital invariants of orders 2 to 10 (Madachy 1979).
| order | RDI | cycle lengths |
| 2 | 4 | 8 |
| 3 | 55, 136, 160, 919 | 3, 2, 3, 2 |
| 4 | 1138, 2178 | 7, 2 |
| 5 | 244, 8294, 8299, 9044, 9045, 10933, | 28, 10, 6, 10, 22, 4, 12, 2, 2 |
| 24584, 58618, 89883 | ||
| 6 | 17148, 63804, 93531, 239459, 282595 | 30, 2, 4, 10, 3 |
| 7 | 80441, 86874, 253074, 376762, | 92, 56, 27, 30, 14, 21 |
| 922428, 982108, five more | ||
| 8 | 6822, 7973187, 8616804 | |
| 9 | 322219, 2274831, 20700388, eleven more | |
| 10 | 20818070, five more |
REFERENCES:
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 163-165, 1979.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|