
NON LINEAR RESTORING FORCES
 المؤلف:
E. R. Huggins
المؤلف:
E. R. Huggins
 المصدر:
Physics 2000
المصدر:
Physics 2000
 الجزء والصفحة:
391
الجزء والصفحة:
391
 2-12-2020
2-12-2020
 3529
3529
NON LINEAR RESTORING FORCES
The simple pendulum is an example of an oscillator with a non linear restoring force. In Figure (1), we show the actual restoring force (mg sin θ) and the linear approximation (mg θ) that we used in order to solve the differential equation for the pendulum’s motion. You can see that if the angle θ always remains small, much less than π/ 2 in magnitude, then the linear force (mg θ) is a good approximation to the non linear force (mg sin θ). Since the linear force gives rise to sinusoidal simple harmonic motion, we expect sinusoidal motion for small oscillations of the simple pendulum. What we are seeing is that a linear restoring force is described by a straight line, and that the non linear restoring force can be approximated by a straight line in the region of small oscillations.
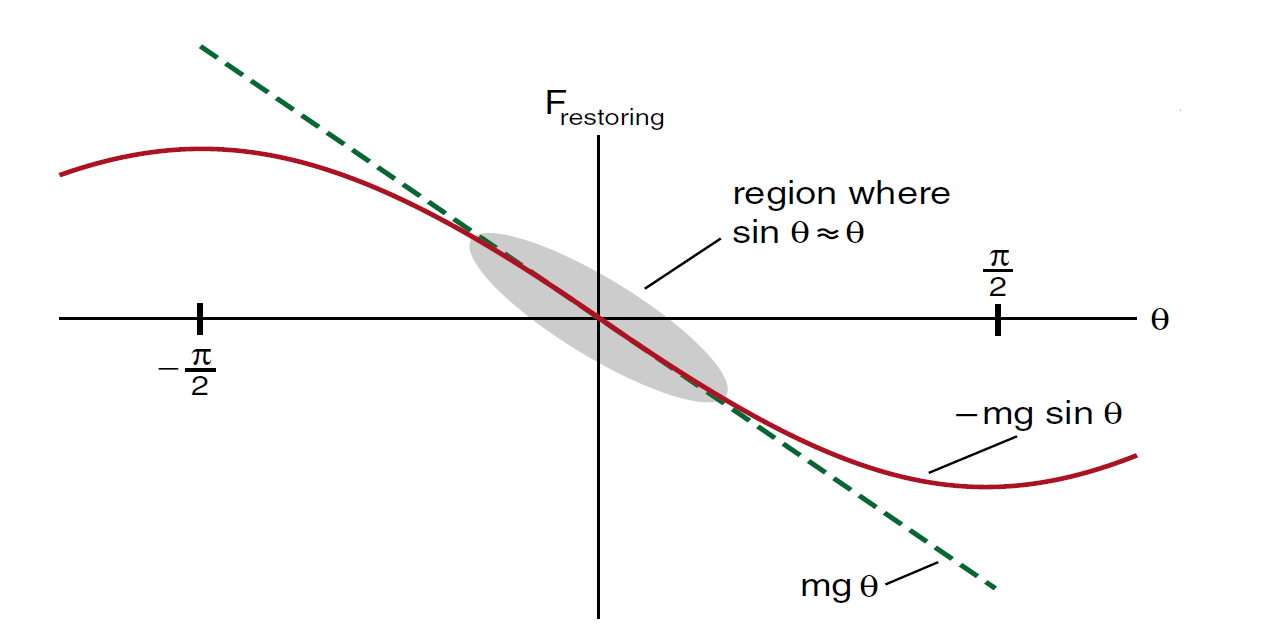
Figure 1: The non linear restoring force mg sinθ can be approximated by the straight line (linear term) mg θ if we keep the angle θ small.
In physics, there are many examples of complex, non linear restoring forces which for small amplitudes can be approximated by a linear restoring force, and which therefore lead to small amplitude sinusoidal oscillations. A rather wild example which we will discuss shortly, is the collapse of the Tacoma Narrows bridge. The bridge undoubtedly started oscillating with small amplitude sinusoidal oscillations. What happened was that these oscillations were continually driven by the shedding wind vortices until the amplitude of oscillation became large and the restoring force was no longer linear. (There was still a more or less sinusoidal motion almost up to the point when the bridge collapsed.)
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


