

|
أقرأ أيضاً
التاريخ: 29-1-2023
التاريخ: 19-1-2023
التاريخ: 2023-07-29
التاريخ: 25-1-2023
|
طريقة مضلع ثايسن Thiessen method
تستخدم هذه الطريقة المساحة المؤثرة لكل محطة قياس في حساب مقدار التساقط طبقاً للطريقة التالية:
1- يرسم موقع كل محطة في خارطة مناسبة.
2- تحدد المساحة المؤثرة لكل محطة على النحو التالي:
- توصل كل محطة مع عدة محطات مجاورة بخطوط مستقيمة.
- تنشأ أعمدة منصفة لكل من هذه الخطوط، وتمد هذه الأعمدة لتقاطع بعضها البعض مكونة مضلع مغلق
حول كل محطة.
3- توجد مساحة المضلع المؤثرة المحيطة بكل محطة بوساطة ممساح أو بأي طريقة أخرى مقبولة لتمثيل المحطة الموجودة بالمساحة هذه المساحة بدقة؛ ويعبر عنها بنسبتها المئوية للمساحة الكلية. وفي حالة وقوع أجزاء من المضلع خارج الحوض الساكب أو في منطقة أخرى يفترض فيها ارتفاع التساقط تقاس المساحة الأجزاء المضلع الواقعة ضمن المساحة قيد البحث.
4- يضرب ارتفاع التساقط في المحطات المختلفة في مساحة المضلع المرتبط بها، ثم تجمع هذه الحسابات ويقسم الناتج على المساحة الكلية لإيجاد التساقط المتوسط.
* تصلح طريقة ثايسن لإيجاد عدد من الارتفاعات المتوسطة لمنطقة معينة تخدم بشبكة من المحطات الثابتة في عددها ومواضعها وتفقد صلاحيتها في حالة إضافة محطات جديدة، أو إخراج محطات من الشبكة، أو في حالة تغير مواضع المحطات أو فقدان بيانات أي محطة. وتقتضي مثل هذه التغيرات إعادة تحديد مضلعات ثايسن لكل المنطقة والمحطات. ومن المفترض عدم استخدام هذه الطريقة في منطقة جبلية للتغير في التساقط المواكب لارتفاع المنطقة. وتبين المعادلة الاتية العملية الحسابية المتبعة في هذه الطريقة.
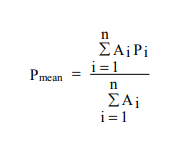
= Pmeanمتوسط الأمطار الهاطلة في المنطقة( ملم(
Pi= تسجيل الأمطار الهاطلة في المحطة i(ملم)
= Ai مساحة المضلع المحيط iبالمحطة الواقعة في منتصفه (م2)
مثال 1
جد التساقط المتوسط في حوض ساكب طبقاً للمعلومات والبيانات الموضحة في الجدول التالي باستخدام طرق مختلفة لتقديرها
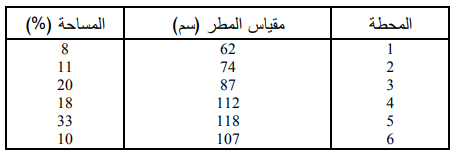
الحل
1- المعطيات: تقديرات الأمطار في المحطات والمساحة.
2- جد متوسط الأمطار الهاطلة بالمنطقة باستخدام طريقة المتوسط الحسابي من المعادلة: 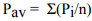
3- جد متوسط الأمطار الهاطلة بالمنطقة باستخدام طريقة ثايسن: 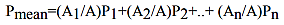
التساقط المتوسط = ( 8×62 + 74×11 + 87×20 + 18×112 + 118×33 + 107×10) / 100 = سم100.3
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|