
Speed as a derivative
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 8
الجزء والصفحة:
Volume I, Chapter 8
 2024-02-04
2024-02-04
 1647
1647
The procedure we have just carried out is performed so often in mathematics that for convenience special notations have been assigned to our quantities ϵ and x. In this notation, the ϵ used above becomes Δt and x becomes Δs. This Δt means “an extra bit of t,” and carries an implication that it can be made smaller. The prefix Δ is not a multiplier, any more than sinθ means s⋅i⋅n⋅θ—it simply defines a time increment, and reminds us of its special character. Δs has an analogous meaning for the distance s. Since Δ is not a factor, it cannot be cancelled in the ratio Δs/Δt to give s/t, any more than the ratio sinθ/sin2θ can be reduced to 1/2 by cancellation. In this notation, velocity is equal to the limit of Δs/Δt when Δt gets smaller, or

This is really the same as our previous expression (8.3) with ϵ and x, but it has the advantage of showing that something is changing, and it keeps track of what is changing.
Incidentally, to a good approximation we have another law, which says that the change in distance of a moving point is the velocity times the time interval, or Δs=vΔt. This statement is true only if the velocity is not changing during that time interval, and this condition is true only in the limit as Δt goes to 0. Physicists like to write it ds=vdt, because by dt they mean Δt in circumstances in which it is very small; with this understanding, the expression is valid to a close approximation. If Δt is too long, the velocity might change during the interval, and the approximation would become less accurate. For a time dt, approaching zero, ds=vdt precisely. In this notation we can write (8.5) as
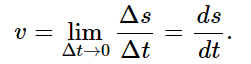
The quantity ds/dt which we found above is called the “derivative of s with respect to t” (this language helps to keep track of what was changed), and the complicated process of finding it is called finding a derivative, or differentiating. The ds’s and dt’s which appear separately are called differentials. To familiarize you with the words, we say we found the derivative of the function 16t2, or the derivative (with respect to t) of 16t2 is 32t. When we get used to the words, the ideas are more easily understood. For practice, let us find the derivative of a more complicated function. We shall consider the formula s=At3+Bt+C, which might describe the motion of a point. The letters A, B, and C represent constant numbers, as in the familiar general form of a quadratic equation. Starting from the formula for the motion, we wish to find the velocity at any time. To find the velocity in the more elegant manner, we change t to t+Δt and note that s is then changed to s+some Δs; then we find the Δs in terms of Δt. That is to say,
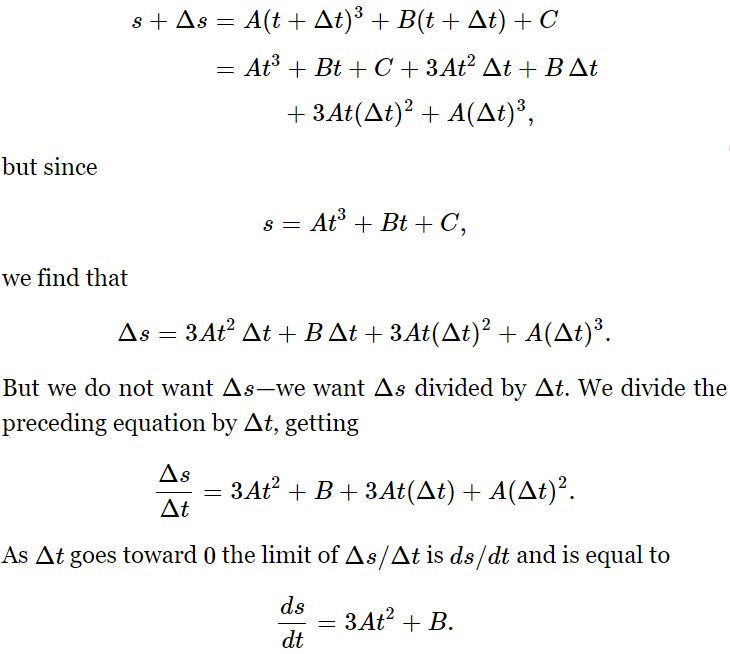
This is the fundamental process of calculus, differentiating functions. The process is even more simple than it appears. Observe that when these expansions contain any term with a square or a cube or any higher power of Δt, such terms may be dropped at once, since they will go to 0 when the limit is taken. After a little practice the process gets easier because one knows what to leave out. There are many rules or formulas for differentiating various types of functions. These can be memorized, or can be found in tables. A short list is found in Table 8–3.
Table 8–3
A Short Table of Derivatives
s, u, v, w are arbitrary functions of t; a, b, c, and n are arbitrary constants

 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


