Newtons Second Law for a System of Particles
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 114
28-12-2016
2613
Newton's Second Law for a System of Particles
For a single particle of mass m we already have encountered Newton's second law, namely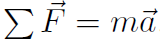 
, and 
are all the forces acting on the mass m and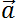 
is the resulting acceleration of the mass m. What happens for a system of particles? The end result is
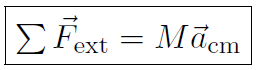(1.1)
where 
is the sum of all external forces acting on the body (all the internal forces cancel out to zero), M is the total mass of the body and 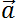cm is the acceleration of the center of mass of the body.
Example Prove equation (1.1).
Solution Recall our definition of center of mass, namely
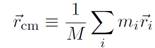
or
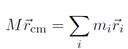
Taking the time derivative gives
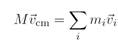
and taking the time derivative again gives
which is just the sum of all the forces acting on each mass mi. These forces will be both external and internal. However for a rigid body all the internal forces must cancel because in a rigid body the particles don't move relative to each other. Thus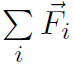 
just becomes 
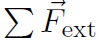in agreement with (1.1).
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
