
Gravitation Near Earths Surface
 المؤلف:
Professor John W. Norbury
المؤلف:
Professor John W. Norbury
 المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
 الجزء والصفحة:
p 159
الجزء والصفحة:
p 159
 29-12-2016
29-12-2016
 2505
2505
Gravitation Near Earth's Surface
Newton's formula  is often called the law of Universal Gravitation because it applies to all bodies in the universe. How does it fit in with our concept of Weight which we defined to be the gravitational force at the surface of the Earth, namely
is often called the law of Universal Gravitation because it applies to all bodies in the universe. How does it fit in with our concept of Weight which we defined to be the gravitational force at the surface of the Earth, namely

where g = 9.8 m sec-1 is the acceleration due to gravity at the surface of the Earth? Well, if  is universal then it should predict the Weight force. Let's see how this comes about.
is universal then it should predict the Weight force. Let's see how this comes about.
Example Show that  gives the same result as W = mg near the surface of Earth.
gives the same result as W = mg near the surface of Earth.
Solution Let m1 ≡ M be the mass of Earth, which is m1 = M = 5:98 × 1024 kg. Let m2 ≡ m be the mass of a person of weight W = mg. The distance between the centers of the masses is just the radius of Earth, i.e. r = 6370 km (which is about 4000 miles, only slightly larger than the width of the United States or Australia). Thus the gravitational force between the two masses is
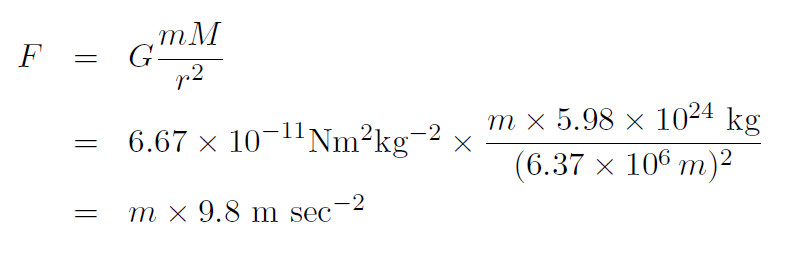
which is the same as W = mg. In other words we have predicted the value of g from the mass and radius of Earth. You could now do the same for the other planets.
Example Explain how to measure the mass of Earth.
Solution In the previous example, we found

where M is the mass of Earth and r is the radius of Earth. Thus by measuring g (which you do in the lab) and by measuring r (which the ancient Greeks knew how to do by comparing the depth of a shadow in a well at two different locations at the same time) then M is given by

and G was measured in the famous Cavendish experiment (look this up).
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


