
تحليل المتجهات Vector Analysis
 المؤلف:
محمد عطية سويلم، د. محمد روبين إدريس، بديع صالح الخطيب، د. أحمد يوسف قواسمة
المؤلف:
محمد عطية سويلم، د. محمد روبين إدريس، بديع صالح الخطيب، د. أحمد يوسف قواسمة
 المصدر:
الفيزياء العامة
المصدر:
الفيزياء العامة
 الجزء والصفحة:
ص 39
الجزء والصفحة:
ص 39
 9-8-2017
9-8-2017
 64664
64664
تحليل المتجهات Vector Analysis
إما أن يكون المتجه في بعد واحد ، كالاتجاه السيني ، أو الصادي ، أو في بعدين ، أي في كلا الاتجاهين ، أوفي ثلاثة أبعاد أو أكثر . ومهما كانت الحالة ، فإنه يمكننا اعتبار أن أي متجه عبارة عن مجموع متجهين أو أكثر . ومجموعة المتجهات التي تجمع لتكون متجها واحدا تسمى مركبات (Components) هذا المتجه.
تسمى عطية جمع متجهين أو أكثر لإعطاء متجه واحد عملية تركيب المتجهات . أما في حالة الاستعاضة عن المتجه بمتجهين أو أكثر ، فإن العملية تسمى تحليل المتجهات . وأسهل الطرق وأكثرها شيوعا في تحليل المتجهات هي استخدام المحاور المتعامدة .
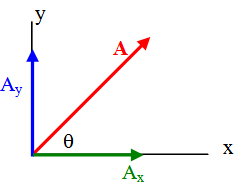
الشكل (1): تحليل المتجه (A) الى مركبتين (Ax) و(Ay)
ففي حالة تحليل المتجه A في البعدين المتعامدين X , Y ، فإن المتجه A يساوي مجموع متجهين متعامدين يتحدان معه في نقطة البداية ، وأحدهما يكون في الاتجاه السيني ، والآخر يكون في الاتجاه الصادي . بحيث يكون المتجه A هو قطر متوازي الأضلاع المكون من المتجهين (المركبتين) , والشكل (13-2) يبين مركبتي المتجه A .
حيث
المركبة السينية (1) ……………………….. Ax = Acos 0
والمركبة الصادية (2) ………………Ay = Asin 0
علمأ بان المتجه (A) هو حاصل جمع المتجهين Ax . Ay
(3) ………………… A= Ax + Ay
ومركبة المتجه في اتجاه ما تعني المسقط العمودي لهذا المتجه على هذا الاتجاه . ولايجاد ذلك ، نسقط عمودا من رأس المتجه ٨ على الاتجاه السيني ، فتكون المركبة في هذا
الاتجاه ٨٢ هي المتجه الواصل من نقطة الأصل الى رأس القائمة (نقطة إسقاط العمود). وبتطبيق نظرية فيثاغورس ، فان :
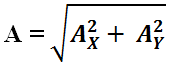 ..................................... (4)
..................................... (4)
إن عملية تحليل المتجهات تفيد في جمع ثلاثة متجهات أو أكثر .
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


