نظام الزوايا نصف قطرية 

‏في هذأ النظام ، تقاس الزوايا بدلالة القوس الذي يقابل الزاوية ونصف قطر الدائرة التي منها هذا القوس : فمثلا الزاوية التي في الشكل (1‏) تساوي بالزوايا القطرية:

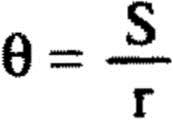..........(1)

‏حيث (S) : طول القوس (AB) . وهذا الاعتبار مبني على أساس أنه لزاوية ما ، تكون النسبة  ثابتة ؛ ولا تتغير بتغير نصف القطر . فإذا زاد طول نصف القطر، مثلا ، فإن طول القوس الذي يقابل الزاوية نفسها يزداد بحيث تبقى النسبة (s/r) ثابتة ؛ ولهذا السبب تم اختيار هذه النسبة لقياس الزوايا في هذا النظام . ومن العلاقة المذكورة أعلاه نستطيع أن نقولθ:S=r

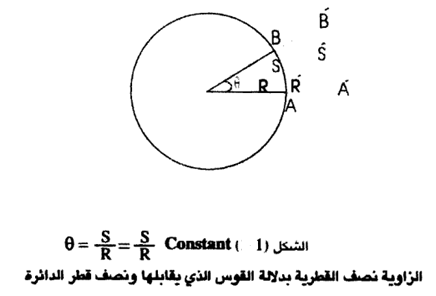
ولما كان محيط الدائرة يساوي " 2rπ"​  حيث (π) هي النسبة التقريبية ، فإننا نجد أن الزاوية الكاملة حول مركز الدائرة والتي يقابلها محيط الدائرة بكامله تساوي π2 (أو 2 ط) زاوية نصف قطرية . أي :

2π radain   360°= 

بمعنى أن 360° درجة في نظام الدرجات تساوي زاوية مقدارها (2π) راديان في نظام الزوايا نصف القطرية . وعليه فإن :

مواضيع ذات صلة

أصول عدم الانعكاس

الانعكاس يولد الانعكاس

الاحتمالية في الميكانيكا الإحصائية

القابلية للانعكاس وعدم القابلية للانعكاس

نظرة في تعددية الفيزياء

الاختزال وعدم القابلية للانعكاس

الواقعية العلمية وتغيير النظريات

نقص الإثبات ومذهب الذرائعية ومذهب الواقعية

مشكلة التمييز: متى يكون المنهج علميا؟

المنهج العلمي: من الاستقراء إلى التكذيب وما بعده

مناهج العلوم وثمارها

!Parity is not conserved