NEWTON’S LAW OF GRAVITY

Newton went beyond using the second law to define force; he also discovered a basic law for the gravitational force between objects. With Newton’s law of gravity combined with Newton’s second law, we can make detailed predictions about how projectiles, satellites, planets, and solar systems behave. This combination, where one has an explicit formula for gravitational forces, and the second law to predict what accelerations these forces produce, was one of the most revolutionary scientific discoveries ever made.
Newton’s so-called universal law of gravitation can most simply be stated as follows. If we have two small masses of mass m₁ and m₂, separated by a distance r as shown in Figure (1), then the force between them is proportional to the product m₁m₂ of their masses, and inversely proportional to the square of the distance r between them. This can be written as an equation of the form
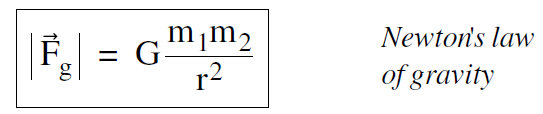.......(1)
where the proportionality constant G is a number that must be determined by experiment.
Equation (3) itself is not the whole story, we must make several more points. First, and very important, is the fact that gravitational forces are always attractive; m₁ is pulled directly toward m₂, and m₂ directly toward m₁. Second, the strength of these forces are equal, even if m₂ is much bigger than m₁, the force of m₂ on m₁ is the same in strength as the force of m₁ on m₂. That is why we used the same symbol for the two attractive forces in Figure (1).

Newton’s law of gravity is called the universal law of gravitation because Equation (1) is supposed to apply to all masses anywhere in the universe, with the same numerical constant G everywhere. G is called the universal gravitational constant, and has the numerical value, in the MKS system of units
..........(2)
We will discuss shortly how this number was first measured.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل