رغم أن قوة الجاذبية تهيمن على حياتنا، فإن تأثيرها على العالم محير من جوانب عدة. دائمًا ما أستعين ببندول لأوضح لطلابي لأي درجة تتنافى آلية عمل الجاذبية مع المنطق.

قد يظن كثيرون منكم أنه إذا تأرجح على أرجوحة بجوار شخص أخف وزنا بكثير، على سبيل المثال: طفل حديث المشي؛ فإن حركة أرجوحة الأول ستكون أبطأ كثيرًا من حركة أرجوحة الشخص الأخف وزنًا. لكن هذا ليس صحيحًا. فقد تفاجؤون بأن الزمن الذي يستغرقه البندول لإكمال حركة تأرجح واحدة، وهو الزمن الذي نطلق عليه دورة البندول؛ لا يتأثر بالوزن الذي يتدلى من البندول (نسمي هذا الوزن المتأرجح الثقل). لاحظ أنني أتكلم هنا عما يسمى بالبندول البسيط، الذي لا بد أن ينطبق عليه شرطان أولا، لا بد أن يكون الوزن المتأرجح أثقل كثيرًا من وزن الوتر الذي يحمله حتى يتسنى لنا تجاهل وزن الوتر. ثانيا، لا بد أن يكون حجم الوزن المتأرجح صغيرًا بما يكفي لاعتباره نقطة صفرية الحجم ⁽¹⁾. من اليسير صناعة بندول بسيط في البيت؛ فما عليك إلا أن تربط تفاحة بوتر خفيف الوزن يبلغ طوله أربعة أمثال حجم التفاحة على الأقل.

باستخدام قوانين نيوتن للحركة أشتق معادلة لحساب زمن البندول البسيط في قاعة الدرس، ثم أختبر تلك المعادلة لتحقيق ذلك يتعين عليَّ افتراض كون الزاوية التي يتأرجح البندول بها زاوية صغيرة. أحتاج هنا لأن أكون شديد التحديد فيما أعني. عندما تنظر إلى البندول الذي صنعته في منزلك وهو يتأرجح من الأمام إلى الخلف أو من اليمين إلى اليسار، ستلاحظ أن البندول في معظم الوقت يتحرك إما إلى اليمين أو إلى اليسار. لكنك ستجده يتوقف تمامًا مرتين خلال كل تأرجح كامل، وستجده يغير اتجاهه عقب كل وقفة عندما يحدث ذلك تكون الزاوية التي بين الوتر والخط العمودي قد بلغت قيمتها القصوى، وهو ما نسميه بسعة البندول. لو كان تجاهل مقاومة الموائع (الاحتكاك) ممكنًا، فحينها ستتساوى الزاوية القصوى التي يتوقف فيها البندول أقصى اليسار مع الزاوية القصوى التي يتوقف عندها البندول أقصى اليمين. لكن المعادلة التي أشتقها هنا لا تصلح إلا للزوايا الصغيرة (السعات الصغيرة). نسمي مثل هذا الاشتقاق في الفيزياء تقارب الزوايا الصغيرة. دائمًا ما يسألني طلابي: «إلى أي مدى يبلغ هذا الصغر؟». بل إن إحداهن كانت أكثر تحديدا في أسئلتها وقالت: «هل تعتبر السعة التي تبلغ خمس درجات صغيرة؟ هل تظل تلك المعادلة صالحة لسعة قدرها عشر درجات أم أن العشر درجات ليست قدرًا صغيرًا؟». تلك أسئلة ممتازة ولا شك، وإنني أقترح أن نجرب الأمر بأنفسنا في قاعة الدرس.

تلك المعادلة التي أشتقها بسيطة جدا وأنيقة جدًّا، رغم أنها قد تبدو مضنيةً لأولئك الذين لم يُجروا أي حسابات رياضية مؤخرًا: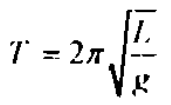

تشير T إلى زمن البندول (بالثواني)، وL هو طول الوتر (بالأمتار)، وتساوي 3.14 وg هو عجلة الجاذبية (9.8 متر في الثانية لكل ثانية). وهكذا، فإن الشطر الأيمن من المعادلة يعني 2π مضروبا في الجذر التربيعي لطول الوتر المقسوم على عجلة الجاذبية. لن أخوض هنا في تفاصيل تؤكد أن هذه. المعادلة الصحيحة. لقد أوردتُ المعادلة هنا ليتسنى لك إدراك مدى الدقة التي تُثبت بها التجارب العملية التي أؤديها في قاعة الدرس صحة المعادلة تتنبأ المعادلة بأن البندول ذا الوتر الذي يبلغ طوله مترًا واحدًا يكون زمنه ثانيتين. لذلك فقد قستُ الوقت الذي يستغرقه بندول بوتر يبلغ هذا الطول لكي يكمل عشر تأرجحات، فكان نحو عشرين ثانية. وعندما نقسم هذا الزمن على 10 فسنجد الأرجحة الواحدة تستغرق نحو ثانيتين. ثم آتي ببندول طول وتره أقصر أربع مرات من طول هذا البندول. فأجد المعادلة تتنبأ بأن زمنه أقصر بمرتين من زمن هذا البندول. لذلك أجعل طول وتر البندول 25 سنتيمترًا فأجد أنه يستغرق بالفعل نحو عشر ثوان ليكمل أرجحة واحدة. وهو ما يؤكد المعادلة.

لاختبار المعادلة بدرجة أدق من اختباري السابق الذي أجريته عن طريق بندول به تفاحة صغيرة، صنعنا بندولا بسيطًا في قاعة الدرس بوتر يبلغ طوله 5.18 متر (نحو 17 قدمًا) وثقل كروي معدني يبلغ 15 كيلوجراما وأسميته البندول الأم.

كم ينبغي أن يكون الزمن T للبندول؟ سيكون 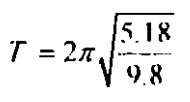، الزمن يساوي حاصل ضرب 2π  في الجذر التربيعي لطول الوتر مقسوما على عجلة الجاذبية، أي 4.75 ثانية. ولاختبار صحة ذلك، كما وعدتُ طلابي قستُ سعتَي الخمس درجات والعشر درجات.

أستخدم في قياسي مؤقتًا رقميًّا كبير الحجم، يستطيع الطلاب رؤيته، وهو مؤقت يعرض الوقت بدقة تبلغ جزءًا من مائة جزء من الثانية وعلى مر السنين كنتُ قد اختبرت زمن ردي للفعل في تشغيل المؤقت وإيقافه عددًا لا له حصر من المرات، وعلمتُ أن قدْرَه جزء على عشرة أجزاء من الثانية (في أحسن الظروف). يعني ذلك أنني لو كررتُ ذات القياس عشرات المرات فسأجده يتباين في الزمن تباينا يبلغ 0.1 ثانية (وربما 0.15 ثانية). لذ فسواء قِسْتُ الزمن اللازم لأرجحة واحدة أو لعشر أرجحات فسيكون الزمن بارتياب يزيد أو يقل عن 0.1 ثانية. ولذلك فقد تركت البندول يتأرجح عشر مرات لأن هذا سينتج عنه قياس أدق بعشر مرات لزمن البندول عنه إذا تركته يتأرجح لمرة واحدة فقط.

أشد ثقل البندول إلى الخارج حتى يصير قدر الزاوية التي يشكلها الخيط مع الخط العمودي نحو خمس درجات، ثم أفلته وأضغط زر المؤقت. يشرع الطلبة في إحصاء كل أرجحة بصوت عال وبعد عشر أرجحات أوقف المؤقت. المدهش أن المؤقت يحسب 45.70 ثانية، أي عشرة أضعاف تقديري للأرجحة الواحدة، وهو ما جعل الطلاب يصفقون بحرارة.

ثم أزيد السعة إلى عشر درجات وأفلت الثقل المتأرجح، ثم أضغط زر المؤقت؛ ويشرع الطلاب في العد، وعقب الأرجحة العاشرة أوقف المؤقت فأجد الرقم الظاهر على شاشته 45.75 ثانية و45.7 ± 0.1 لعشر أرجحات يعني 4.575 ± 0.01 ثانية لكل أرجحة مما يعني أن نتيجة سعة الخمس درجات هي نفسها نتيجة سعة العشر درجات (مع نسبة ارتياب في القياسات). وهكذا فإن قياساتي ما تزال دقيقة.

ثم أسأل الطلبة أن يفترضوا أنني جلستُ على الثقل وتأرجحت معه، فهل سنخرج بنفس الزمن حينها أم أنه سيتغير؟ بالطبع لا أريد أن أجلس على ذلك الشيء (فهو أمر مؤلم للغاية، لكن لأجل العلم ولأجل إضحاك الطلبة ودمجهم في التجربة فلن أفوت هذه الفرصة. بالطبع لا يمكنني أن أجلس منتصبا على الثقل؛ لأن ذلك سوف يؤدي إلى تقصير الحبل وتقليل الزمن قليلا لكنني لو جعلتُ جسمي في الوضع الأفقي قدر الاستطاعة كي يكون على نفس مستوى الثقل، فإنني أحافظ على طول الحبل كما هو تقريبا. لذلك أجذب الثقل لأعلى وأضعه بين رجلي وأمسك بالحبل ثم أطلق العنان لنفسي.

ليس من اليسير علي أن أشغل المؤقت وأوقفه وأنا أتعلق في البندول دون أن أزيد من زمن رد الفعل. لكنني قد تدربت على ذلك مرات كثيرة، لدرجة أنني صرت على شبه يقين من أن مقدار الارتياب الذي يمكن تحقيقه في قياساتي ± 0.1 ثانية. أتأرجح عشر مرات وطلبتي يعدون الأرجحات ويتضاحكون من عبثية موقفي ذلك، وأنا أتذمر وأزمجر بصوت عال ثم أوقف المؤقت عقب إكمال الأرجحات العشر، فأجده يسجل 45.61 ثانية. وهو ما يعني 4.56 ± 0.01 ثانية. أصبح عاليا «الفيزياء حق» فتضج القاعة بحماس الطلاب.

________________________________________________
هوامش

(1) لو لم يتسن تجاهل كتلة الوتر ولم تتسن معاملة حجم الوزن المتأرجح على أنه كتلة نقطية، حينها لن يعتبر هذا البندول بسيطاً. حينها سنسميه بندولا فيزيائيا وسيسلك سلوكا مختلفا.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل