
Short times
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 5
الجزء والصفحة:
Volume I, Chapter 5
 2024-01-27
2024-01-27
 1915
1915
We should now notice that in the process of checking on the reproducibility of the day, we have received an important by-product. We have found a way of measuring, more accurately, fractions of a day. We have found a way of counting time in smaller pieces. Can we carry the process further, and learn to measure even smaller intervals of time?
Galileo decided that a given pendulum always swings back and forth in equal intervals of time so long as the size of the swing is kept small. A test comparing the number of swings of a pendulum in one “hour” shows that such is indeed the case. We can in this way mark fractions of an hour. If we use a mechanical device to count the swings—and to keep them going—we have the pendulum clock of our grandfathers.
Let us agree that if our pendulum oscillates 3600 times in one hour (and if there are 24 such hours in a day), we shall call each period of the pendulum one “second.” We have then divided our original unit of time into approximately 105 parts. We can apply the same principles to divide the second into smaller and smaller intervals. It is, you will realize, not practical to make mechanical pendulums which go arbitrarily fast, but we can now make electrical pendulums, called oscillators, which can provide a periodic occurrence with a very short period of swing. In these electronic oscillators it is an electrical current which swings to and forth, in a manner analogous to the swinging of the bob of the pendulum.
We can make a series of such electronic oscillators, each with a period 10 times shorter than the previous one. We may “calibrate” each oscillator against the next slower one by counting the number of swings it makes for one swing of the slower oscillator. When the period of oscillation of our clock is shorter than a fraction of a second, we cannot count the oscillations without the help of some device which extends our powers of observation. One such device is the electron-beam oscilloscope, which acts as a sort of microscope for short times. This device plots on a fluorescent screen a graph of electrical current (or voltage) versus time. By connecting the oscilloscope to two of our oscillators in sequence, so that it plots a graph first of the current in one of our oscillators and then of the current in the other, we get two graphs like those shown in Fig. 5–2. We can readily determine the number of periods of the faster oscillator in one period of the slower oscillator.
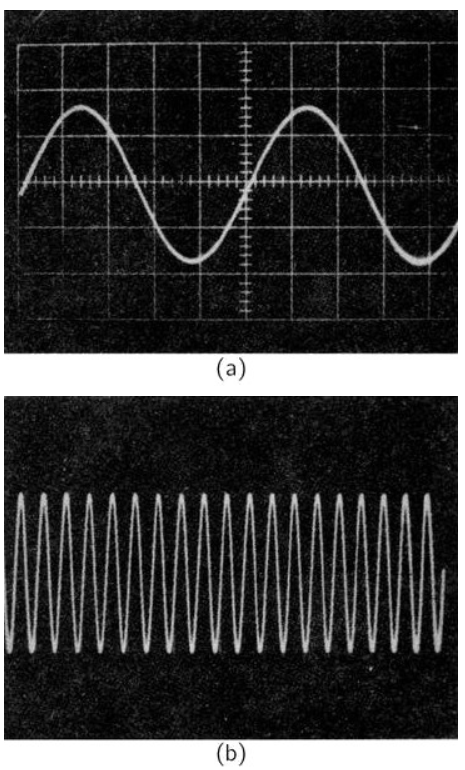
Fig. 5–2. Two views of an oscilloscope screen. In (a) the oscilloscope is connected to one oscillator, in (b) it is connected to an oscillator with a period one-tenth as long.
With modern electronic techniques, oscillators have been built with periods as short as about 10−12 second, and they have been calibrated (by comparison methods such as we have described) in terms of our standard unit of time, the second. With the invention and perfection of the “laser,” or light amplifier, in the past few years, it has become possible to make oscillators with even shorter periods than 10−12 second, but it has not yet been possible to calibrate them by the methods which have been described, although it will no doubt soon be possible.
Times shorter than 10−12 second have been measured, but by a different technique. In effect, a different definition of “time” has been used. One way has been to observe the distance between two happenings on a moving object. If, for example, the headlights of a moving automobile are turned on and then off, we can figure out how long the lights were on if we know where they were turned on and off and how fast the car was moving. The time is the distance over which the lights were on divided by the speed.
Within the past few years, just such a technique was used to measure the lifetime of the π0–meson. By observing in a microscope, the minute tracks left in a photographic emulsion in which π0–meson had been created one saw that a π0–meson (known to be travelling at a certain speed nearly that of light) went a distance of about 10−7 meter, on the average, before disintegrating. It lived for only about 10−16 sec. It should be emphasized that we have here used a somewhat different definition of “time” than before. So long as there are no inconsistencies in our understanding, however, we feel fairly confident that our definitions are sufficiently equivalent.
By extending our techniques—and if necessary, our definitions—still further we can infer the time duration of still faster physical events. We can speak of the period of a nuclear vibration. We can speak of the lifetime of the newly discovered strange resonances (particles) mentioned in Chapter 2. Their complete life occupies a time span of only 10−24 second, approximately the time it would take light (which moves at the fastest known speed) to cross the nucleus of hydrogen (the smallest known object).
What about still smaller times? Does “time” exist on a still smaller scale? Does it make any sense to speak of smaller times if we cannot measure—or perhaps even think sensibly about—something which happens in a shorter time? Perhaps not. These are some of the open questions which you will be asking and perhaps answering in the next twenty or thirty years.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


