
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Pseudo forces
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 12
2024-02-13
1809
The next kind of force we shall discuss might be called a pseudo force. There is relationship between two people, Joe and Moe, who use different coordinate systems. Let us suppose that the positions of a particle as measured by Joe are x and by Moe are x′; then the laws are as follows:
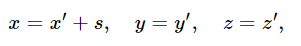
where s is the displacement of Moe’s system relative to Joe’s. If we suppose that the laws of motion are correct for Joe, how do they look for Moe? We find first, that
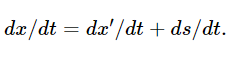
Previously, we considered the case where s was constant, and we found that s made no difference in the laws of motion, since ds/dt=0; ultimately, therefore, the laws of physics were the same in both systems. But another case we can take is that s=ut, where u is a uniform velocity in a straight line. Then s is not constant, and ds/dt is not zero, but is u, a constant. However, the acceleration d2x/dt2 is still the same as d2x′/dt2, because du/dt=0. This proves the law that we used in Chapter 10, namely, that if we move in a straight line with uniform velocity the laws of physics will look the same to us as when we are standing still. That is the Galilean transformation. But we wish to discuss the interesting case where s is still more complicated, say s=at2/2. Then ds/dt=at and d2s/dt2=a, a uniform acceleration; or in a still more complicated case, the acceleration might be a function of time. This means that although the laws of motion from the point of view of Joe would look like
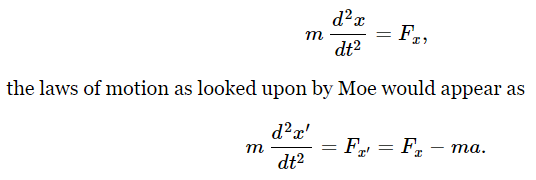
That is, since Moe’s coordinate system is accelerating with respect to Joe’s, the extra term ma comes in, and Moe will have to correct his forces by that amount in order to get Newton’s laws to work. In other words, here is an apparent, mysterious new force of unknown origin which arises, of course, because Moe has the wrong coordinate system. This is an example of a pseudo force; other examples occur in coordinate systems that are rotating.
Another example of pseudo force is what is often called “centrifugal force.” An observer in a rotating coordinate system, e.g., in a rotating box, will find mysterious forces, not accounted for by any known origin of force, throwing things outward toward the walls. These forces are due merely to the fact that the observer does not have Newton’s coordinate system, which is the simplest coordinate system.
Pseudo force can be illustrated by an interesting experiment in which we push a jar of water along a table, with acceleration. Gravity, of course, acts downward on the water, but because of the horizontal acceleration there is also a pseudo force acting horizontally and in a direction opposite to the acceleration. The resultant of gravity and pseudo force makes an angle with the vertical, and during the acceleration the surface of the water will be perpendicular to the resultant force, i.e., inclined at an angle with the table, with the water standing higher in the rearward side of the jar. When the push on the jar stops and the jar decelerates because of friction, the pseudo force is reversed, and the water stands higher in the forward side of the jar (Fig. 12–4).
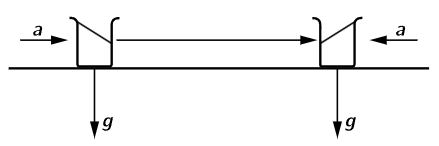
Fig. 12–4. Illustration of a pseudo force.
One very important feature of pseudo forces is that they are always proportional to the masses; the same is true of gravity. The possibility exists, therefore, that gravity itself is a pseudo force. Is it not possible that perhaps gravitation is due simply to the fact that we do not have the right coordinate system? After all, we can always get a force proportional to the mass if we imagine that a body is accelerating. For instance, a man shut up in a box that is standing still on the earth finds himself held to the floor of the box with a certain force that is proportional to his mass. But if there were no earth at all and the box were standing still, the man inside would float in space. On the other hand, if there were no earth at all and something were pulling the box along with an acceleration g, then the man in the box, analyzing physics, would find a pseudo force which would pull him to the floor, just as gravity does.
Einstein put forward the famous hypothesis that accelerations give an imitation of gravitation, that the forces of acceleration (the pseudo forces) cannot be distinguished from those of gravity; it is not possible to tell how much of a given force is gravity and how much is pseudo force.
It might seem all right to consider gravity to be a pseudo force, to say that we are all held down because we are accelerating upward, but how about the people in Madagascar, on the other side of the earth—are they accelerating too? Einstein found that gravity could be considered a pseudo force only at one point at a time, and was led by his considerations to suggest that the geometry of the world is more complicated than ordinary Euclidean geometry. The present discussion is only qualitative, and does not pretend to convey anything more than the general idea. To give a rough idea of how gravitation could be the result of pseudo forces, we present an illustration which is purely geometrical and does not represent the real situation. Suppose that we all lived in two dimensions, and knew nothing of a third. We think we are on a plane, but suppose we are really on the surface of a sphere. And suppose that we shoot an object along the ground, with no forces on it. Where will it go? It will appear to go in a straight line, but it has to remain on the surface of a sphere, where the shortest distance between two points is along a great circle; so, it goes along a great circle. If we shoot another object similarly, but in another direction, it goes along another great circle. Because we think we are on a plane, we expect that these two bodies will continue to diverge linearly with time, but careful observation will show that if they go far enough, they move closer together again, as though they were attracting each other. But they are not attracting each other—there is just something “weird” about this geometry. This particular illustration does not describe correctly the way in which Einstein’s geometry is “weird,” but it illustrates that if we distort the geometry sufficiently it is possible that all gravitation is related in some way to pseudo forces; that is the general idea of the Einsteinian theory of gravitation.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















