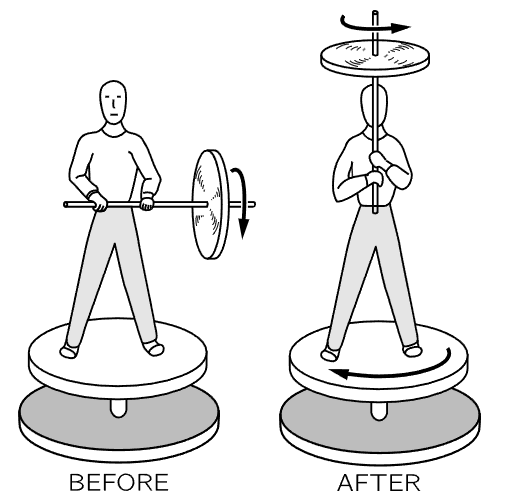
Fig. 20–1. Before: axis is horizontal; momentum about vertical axis=0. After: axis is vertical; momentum about vertical axis is still zero; man, and chair spin in direction opposite to spin of the wheel.
Let us return to the law of conservation of angular momentum. This law may be demonstrated with a rapidly spinning wheel, or gyroscope, as follows (see Fig. 20–1). If we sit on a swivel chair and hold the spinning wheel with its axis horizontal, the wheel has an angular momentum about the horizontal axis. Angular momentum around a vertical axis cannot change because of the (frictionless) pivot of the chair, so if we turn the axis of the wheel into the vertical, then the wheel would have angular momentum about the vertical axis, because it is now spinning about this axis. But the system (wheel, ourself, and chair) cannot have a vertical component, so we and the chair have to turn in the direction opposite to the spin of the wheel, to balance it.
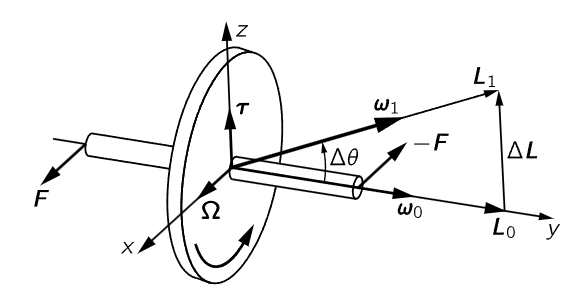
Fig. 20–2. A gyroscope.
First let us analyze in more detail the thing we have just described. What is surprising, and what we must understand, is the origin of the forces which turn us and the chair around as we turn the axis of the gyroscope toward the vertical. Figure 20–2 shows the wheel spinning rapidly about the y-axis. Therefore, its angular velocity is about that axis and, it turns out, its angular momentum is likewise in that direction. Now suppose that we wish to rotate the wheel about the x-axis at a small angular velocity Ω; what forces are required? After a short time Δt, the axis has turned to a new position, tilted at an angle Δθ with the horizontal. Since the major part of the angular momentum is due to the spin on the axis (very little is contributed by the slow turning), we see that the angular momentum vector has changed. What is the change in angular momentum? The angular momentum does not change in magnitude, but it does change in direction by an amount Δθ. The magnitude of the vector ΔL is thus ΔL=L0Δθ, so that the torque, which is the time rate of change of the angular momentum, is τ=ΔL/Δt=L0Δθ/Δt=L0Ω. Taking the directions of the various quantities into account, we see that

Thus, if Ω and L0 are both horizontal, as shown in the figure, τ is vertical. To produce such a torque, horizontal forces F and −F must be applied at the ends of the axle. How are these forces applied? By our hands, as we try to rotate the axis of the wheel into the vertical direction. But Newton’s Third Law demands that equal and opposite forces (and equal and opposite torques) act on us. This causes us to rotate in the opposite sense about the vertical axis z.

Fig. 20–3. A rapidly spinning top. Note that the direction of the torque vector is the direction of the precession.
This result can be generalized for a rapidly spinning top. In the familiar case of a spinning top, gravity acting on its center of mass furnishes a torque about the point of contact with the floor (see Fig. 20–3). This torque is in the horizontal direction, and causes the top to precess with its axis moving in a circular cone about the vertical. If Ω is the (vertical) angular velocity of precession, we again find that
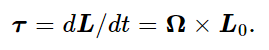
Thus, when we apply a torque to a rapidly spinning top, the direction of the precessional motion is in the direction of the torque, or at right angles to the forces producing the torque.
We may now claim to understand the precession of gyroscopes, and indeed we do, mathematically. However, this is a mathematical thing which, in a sense, appears as a “miracle.” It will turn out, as we go to more and more advanced physics, that many simple things can be deduced mathematically more rapidly than they can be really understood in a fundamental or simple sense. This is a strange characteristic, and as we get into more and more advanced work there are circumstances in which mathematics will produce results which no one has really been able to understand in any direct fashion. An example is the Dirac equation, which appears in a very simple and beautiful form, but whose consequences are hard to understand. In our particular case, the precession of a top looks like some kind of a miracle involving right angles and circles, and twists and right-hand screws. What we should try to do is to understand it in a more physical way.

Fig. 20–4. The motion of particles in the spinning wheel of Fig. 20–2, whose axis is turning, is in curved lines.
How can we explain the torque in terms of the real forces and the accelerations? We note that when the wheel is precessing, the particles that are going around the wheel are not really moving in a plane because the wheel is precessing (see Fig. 20–4). As we explained previously (Fig. 19–4), the particles which are crossing through the precession axis are moving in curved paths, and this requires application of a lateral force. This is supplied by our pushing on the axle, which then communicates the force to the rim through the spokes. “Wait,” someone says, “what about the particles that are going back on the other side?” It does not take long to decide that there must be a force in the opposite direction on that side. The net force that we have to apply is therefore zero. The forces balance out, but one of them must be applied at one side of the wheel, and the other must be applied at the other side of the wheel. We could apply these forces directly, but because the wheel is solid, we are allowed to do it by pushing on the axle, since forces can be carried up through the spokes.
What we have so far proved is that if the wheel is precessing, it can balance the torque due to gravity or some other applied torque. But all we have shown is that this is a solution of an equation. That is, if the torque is given, and if we get the spinning started right, then the wheel will precess smoothly and uniformly. But we have not proved (and it is not true) that a uniform precession is the most general motion a spinning body can undergo as the result of a given torque. The general motion involves also a “wobbling” about the mean precession. This “wobbling” is called nutation.
Some people like to say that when one exerts a torque on a gyroscope, it turns and it precesses, and that the torque produces the precession. It is very strange that when one suddenly let's go of a gyroscope, it does not fall under the action of gravity, but moves sidewise instead! Why is it that the downward force of the gravity, which we know and feel, makes it go sidewise? All the formulas in the world like (20.15) are not going to tell us, because (20.15) is a special equation, valid only after the gyroscope is precessing nicely. What really happens, in detail, is the following. If we were to hold the axis absolutely fixed, so that it cannot precess in any manner (but the top is spinning) then there is no torque acting, not even a torque from gravity, because it is balanced by our fingers. But if we suddenly let go, then there will instantaneously be a torque from gravity. Anyone in his right mind would think that the top would fall, and that is what it starts to do, as can be seen if the top is not spinning too fast.
The gyro actually does fall, as we would expect. But as soon as it falls, it is then turning, and if this turning were to continue, a torque would be required. In the absence of a torque in this direction, the gyro begins to “fall” in the direction opposite that of the missing force. This gives the gyro a component of motion around the vertical axis, as it would have in steady precession. But the actual motion “overshoots” the steady precessional velocity, and the axis actually rises again to the level from which it started. The path followed by the end of the axle is a cycloid (the path followed by a pebble that is stuck in the tread of an automobile tire). Ordinarily, this motion is too quick for the eye to follow, and it damps out quickly because of the friction in the gimbal bearings, leaving only the steady precessional drift (Fig. 20–5). The slower the wheel spins, the more obvious the nutation is.
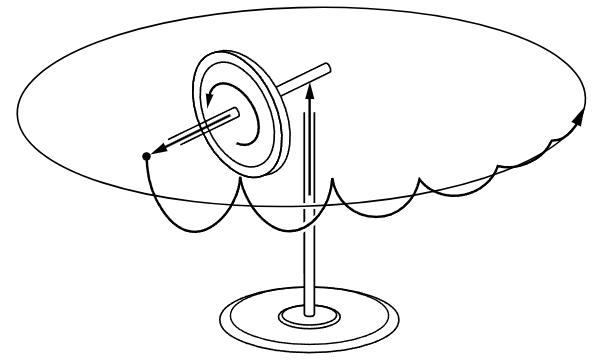
Fig. 20–5. Actual motion of tip of axis of gyroscope under gravity just after releasing axis previously held fixed.
When the motion settles down, the axis of the gyro is a little bit lower than it was at the start. Why? (These are the more complicated details, but we bring them in because we do not want the reader to get the idea that the gyroscope is an absolute miracle. It is a wonderful thing, but it is not a miracle.) If we were holding the axis absolutely horizontally, and suddenly let go, then the simple precession equation would tell us that it precesses, that it goes around in a horizontal plane. But that is impossible! Although we neglected it before, it is true that the wheel has some moment of inertia about the precession axis, and if it is moving about that axis, even slowly, it has a weak angular momentum about the axis. Where did it come from? If the pivots are perfect, there is no torque about the vertical axis. How then does it get to precess if there is no change in the angular momentum? The answer is that the cycloidal motion of the end of the axis damps down to the average, steady motion of the center of the equivalent rolling circle. That is, it settles down a little bit low. Because it is low, the spin angular momentum now has a small vertical component, which is exactly what is needed for the precession. So you see it has to go down a little, in order to go around. It has to yield a little bit to the gravity; by turning its axis down a little bit, it maintains the rotation about the vertical axis. That, then, is the way a gyroscope works.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


