
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Complex numbers and harmonic motion
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 23
2024-03-10
2252
In the present chapter we shall continue our discussion of the harmonic oscillator and, in particular, the forced harmonic oscillator, using a new technique in the analysis. In the preceding chapter we introduced the idea of complex numbers, which have real and imaginary parts and which can be represented on a diagram in which the ordinate represents the imaginary part and the abscissa represents the real part. If a is a complex number, we may write it as a=ar+iai, where the subscript r means the real part of a, and the subscript i means the imaginary part of a. Referring to Fig. 23–1, we see that we may also write a complex number a=x+iy in the form x+iy=reiθ, where r2=x2+y2=(x+iy)(x−iy)=aa∗. (The complex conjugate of a, written a∗, is obtained by reversing the sign of i in a.) So, we shall represent a complex number in either of two forms, a real plus an imaginary part, or a magnitude r and a phase angle θ, so-called. Given r and θ, x and y are clearly r cosθ and r sinθ and, in reverse, given a complex number 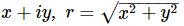 and tanθ=y/x, the ratio of the imaginary to the real part.
and tanθ=y/x, the ratio of the imaginary to the real part.
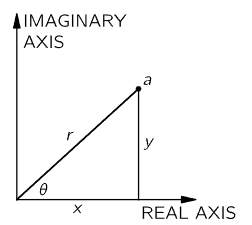
Fig. 23–1. A complex number may be represented by a point in the “complex plane.”
We are going to apply complex numbers to our analysis of physical phenomena by the following trick. We have examples of things that oscillate; the oscillation may have a driving force which is a certain constant times cos ωt. Now such a force, F=F0 cos ωt, can be written as the real part of a complex number F=F0eiωt because eiωt = cos ωt+i sin ωt. The reason we do this is that it is easier to work with an exponential function than with a cosine. So, the whole trick is to represent our oscillatory functions as the real parts of certain complex functions. The complex number F that we have so defined is not a real physical force, because no force in physics is really complex; actual forces have no imaginary part, only a real part. We shall, however, speak of the “force” F0 eiωt, but of course the actual force is the real part of that expression.
Let us take another example. Suppose we want to represent a force which is a cosine wave that is out of phase with a delayed phase Δ. This, of course, would be the real part of F0ei(ωt−Δ), but exponentials being what they are, we may write ei(ωt−Δ) = eiωte−iΔ. Thus, we see that the algebra of exponentials is much easier than that of sines and cosines; this is the reason we choose to use complex numbers. We shall often write

We write a little caret (^) over the F to remind ourselves that this quantity is a complex number: here the number is

Now let us solve an equation, using complex numbers, to see whether we can work out a problem for some real case. For example, let us try to solve
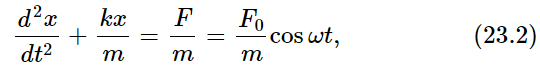
where F is the force which drives the oscillator and x is the displacement. Now, absurd though it may seem, let us suppose that x and F are actually complex numbers, for a mathematical purpose only. That is to say, x has a real part and an imaginary part times i, and F has a real part and an imaginary part times i. Now if we had a solution of (23.2) with complex numbers, and substituted the complex numbers in the equation, we would get
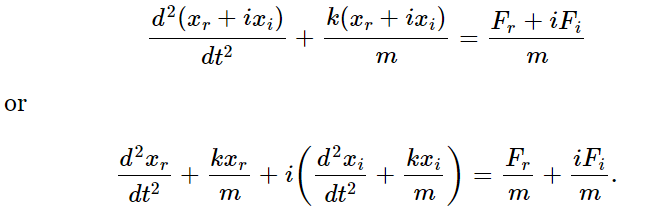
Now, since if two complex numbers are equal, their real parts must be equal and their imaginary parts must be equal, we deduce that the real part of x satisfies the equation with the real part of the force. We must emphasize, however, that this separation into a real part and an imaginary part is not valid in general, but is valid only for equations which are linear, that is, for equations in which x appears in every term only in the first power or the zeroth power. For instance, if there were in the equation a term λx2, then when we substitute xr+ixi, we would get λ(xr+ixi)2, but when separated into real and imaginary parts this would yield λ(x2r−x2i) as the real part and 2iλxrxi as the imaginary part. So, we see that the real part of the equation would not involve just λx2r, but also −λx2i. In this case we get a different equation than the one we wanted to solve, with xi, the completely artificial thing we introduced in our analysis, mixed in.
Let us now try our new method for the problem of the forced oscillator, that we already know how to solve. We want to solve Eq. (23.2) as before, but we say that we are going to try to solve
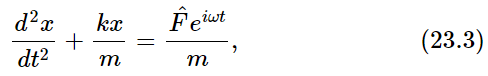
where  is a complex number. Of course x will also be complex, but remember the rule: take the real part to find out what is really going on. So we try to solve (23.3) for the forced solution; we shall discuss other solutions later. The forced solution has the same frequency as the applied force, and has some amplitude of oscillation and some phase, and so it can be represented also by some complex number
is a complex number. Of course x will also be complex, but remember the rule: take the real part to find out what is really going on. So we try to solve (23.3) for the forced solution; we shall discuss other solutions later. The forced solution has the same frequency as the applied force, and has some amplitude of oscillation and some phase, and so it can be represented also by some complex number 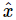 whose magnitude represents the swing of x and whose phase represents the time delay in the same way as for the force. Now a wonderful feature of an exponential function
whose magnitude represents the swing of x and whose phase represents the time delay in the same way as for the force. Now a wonderful feature of an exponential function  is that dx/dt=iωx. When we differentiate an exponential function, we bring down the exponent as a simple multiplier. The second derivative does the same thing, it brings down another iω, and so it is very simple to write immediately, by inspection, what the equation is for x: every time we see a differentiation, we simply multiply by iω. (Differentiation is now as easy as multiplication! This idea of using exponentials in linear differential equations is almost as great as the invention of logarithms, in which multiplication is replaced by addition. Here differentiation is replaced by multiplication.) Thus our equation becomes
is that dx/dt=iωx. When we differentiate an exponential function, we bring down the exponent as a simple multiplier. The second derivative does the same thing, it brings down another iω, and so it is very simple to write immediately, by inspection, what the equation is for x: every time we see a differentiation, we simply multiply by iω. (Differentiation is now as easy as multiplication! This idea of using exponentials in linear differential equations is almost as great as the invention of logarithms, in which multiplication is replaced by addition. Here differentiation is replaced by multiplication.) Thus our equation becomes

(We have cancelled the common factor eiωt.) See how simple it is! Differential equations are immediately converted, by sight, into mere algebraic equations; we virtually have the solution by sight, that
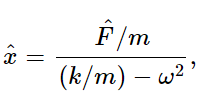
since (iω)2=−ω2. This may be slightly simplified by substituting k/m=ω20, which gives
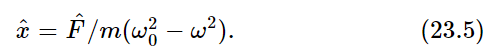
This, of course, is the solution we had before; for since m(ω20−ω2) is a real number, the phase angles of 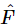 and of
and of  are the same (or perhaps 180∘ apart, if ω2>ω20), as advertised previously. The magnitude of
are the same (or perhaps 180∘ apart, if ω2>ω20), as advertised previously. The magnitude of 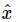 , which measures how far it oscillates, is related to the size of the
, which measures how far it oscillates, is related to the size of the  by the factor 1/m(ω20−ω2), and this factor becomes enormous when ω is nearly equal to ω0. So we get a very strong response when we apply the right frequency ω (if we hold a pendulum on the end of a string and shake it at just the right frequency, we can make it swing very high).
by the factor 1/m(ω20−ω2), and this factor becomes enormous when ω is nearly equal to ω0. So we get a very strong response when we apply the right frequency ω (if we hold a pendulum on the end of a string and shake it at just the right frequency, we can make it swing very high).
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















