
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The exponential atmosphere
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 40
2024-05-17
1741
We already have one of the theorems of statistical echanics, namely, the mean value of the kinetic energy for any motion at the absolute temperature T is 1/2 kT for each ndependent motion, i.e., for each degree of freedom. That tells us something about the mean square velocities of the atoms. Our objective now is to learn more about the positions of the atoms, to discover how many of them are going to be in different places at thermal equilibrium, and also to go into a little more detail on the distribution of the velocities. Although we have the mean square velocity, we do not know how to answer a question such as how many of them are going three times faster than the root mean square, or how many of them are going one-quarter of the root mean square speed. Or have they all the same speed exactly?
So, these are the two questions that we shall try to answer: How are the molecules distributed in space when there are forces acting on them, and how are they distributed in velocity?
It turns out that the two questions are completely independent, and that the distribution of velocities is always the same. We already received a hint of the latter fact when we found that the average kinetic energy is the same, 12kT
per degree of freedom, no matter what forces are acting on the molecules. The distribution of the velocities of the molecules is independent of the forces, because the collision rates do not depend upon the forces.
Let us begin with an example: the distribution of the molecules in an atmosphere like our own, but without the winds and other kinds of disturbance. Suppose that we have a column of gas extending to a great height, and at thermal equilibrium—unlike our atmosphere, which as we know gets colder as we go up. We could remark that if the temperature differed at different heights, we could demonstrate lack of equilibrium by connecting a rod to some balls at the bottom (Fig. 40–1), where they would pick up 1/2 kT from the molecules there and would shake, via the rod, the balls at the top and those would shake the molecules at the top. So, ultimately, of course, the temperature becomes the same at all heights in a gravitational field.

Fig. 40–1. The pressure at height h must exceed that at h+dh by the weight of the intervening gas.
If the temperature is the same at all heights, the problem is to discover by what law the atmosphere becomes tenuous as we go up. If N is the total number of molecules in a volume V of gas at pressure P, then we know PV=NkT, or P=nkT, where n=N/V is the number of molecules per unit volume. In other words, if we know the number of molecules per unit volume, we know the pressure, and vice versa: they are proportional to each other, since the temperature is constant in this problem. But the pressure is not constant, it must increase as the altitude is reduced, because it has to hold, so to speak, the weight of all the gas above it. That is the clue by which we may determine how the pressure changes with height. If we take a unit area at height h, then the vertical force from below, on this unit area, is the pressure P. The vertical force per unit area pushing down at a height h+dh would be the same, in the absence of gravity, but here it is not, because the force from below must exceed the force from above by the weight of gas in the section between h and h+dh. Now mg is the force of gravity on each molecule, where g is the acceleration due to gravity, and ndh is the total number of molecules in the unit section. So this gives us the differential equation Ph+dh−Ph= dP= −mgndh. Since P=nkT, and T is constant, we can eliminate either P or n, say P, and get
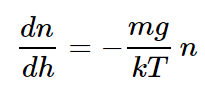
for the differential equation, which tells us how the density goes down as we go up in energy.
We thus have an equation for the particle density n, which varies with height, but which has a derivative which is proportional to itself. Now a function which has a derivative proportional to itself is an exponential, and the solution of this differential equation is

Here the constant of integration, n0, is obviously the density at h=0 (which can be chosen anywhere), and the density goes down exponentially with height.

Fig. 40–2. The normalized density as a function of height in the earth’s gravitational field for oxygen and for hydrogen, at constant temperature.
Note that if we have different kinds of molecules with different masses, they go down with different exponentials. The ones which were heavier would decrease with altitude faster than the light ones. Therefore, we would expect that because oxygen is heavier than nitrogen, as we go higher and higher in an atmosphere with nitrogen and oxygen the proportion of nitrogen would increase. This does not really happen in our own atmosphere, at least at reasonable heights, because there is so much agitation which mixes the gases back together again. It is not an isothermal atmosphere. Nevertheless, there is a tendency for lighter materials, like hydrogen, to dominate at very great heights in the atmosphere, because the lowest masses continue to exist, while the other exponentials have all died out (Fig. 40–2).
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















