
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Bow waves
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 51
2024-06-30
1149
Although we have finished our quantitative analyses of waves, this added chapter on the subject is intended to give some appreciation, qualitatively, for various phenomena that are associated with waves, which are too complicated to analyze in detail here. Since we have been dealing with waves for several chapters, more properly the subject might be called “some of the more complex phenomena associated with waves.”
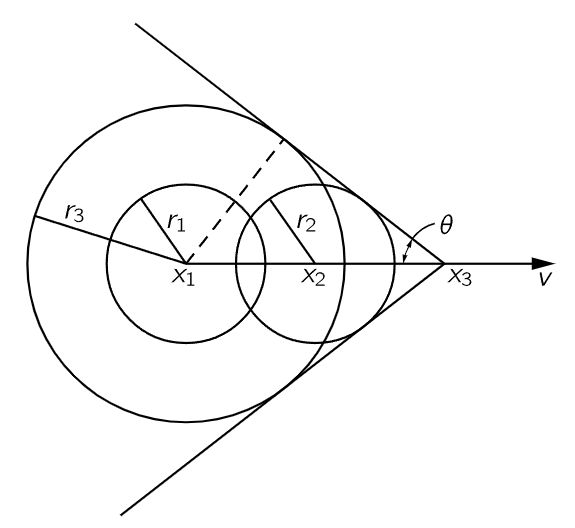
Fig. 51–1. The shock wave front lies on a cone with apex at the source and half-angle θ=sin−1cw/v.
The first topic to be discussed concerns the effects that are produced by a source of waves which is moving faster than the wave velocity, or the phase velocity. Let us first consider waves that have a definite velocity, like sound and light. If we have a source of sound which is moving faster than the speed of sound, then something like this happens: Suppose at a given moment a sound wave is generated from the source at point x1 in Fig. 51–1; then, in the next moment, as the source moves to x2, the wave from x1 expands by a radius r1 smaller than the distance that the source moves; and, of course, another wave starts from x2. When the sound source has moved still farther, to x3, and a wave is starting there, the wave from x2 has now expanded to r2, and the one from x1 has expanded to r3. Of course, the thing is done continuously, not in steps, and therefore, we have a series of wave circles with a common tangent line which goes through the center of the source. We see that instead of a source generating spherical waves, as it would if it were standing still, it generates a wavefront which forms a cone in three dimensions, or a pair of lines in two dimensions. The angle of the cone is very easy to figure out. In a given amount of time the source moves a distance, say x3−x1, proportional to v, the velocity of the source. In the meantime, the wavefront has moved out a distance r3, proportional to cw, the speed of the wave. Therefore, it is clear that the half-angle of opening has a sine equal to the ratio of the speed of the waves, divided by the speed of the source, and this sine has a solution only if cw is less than v, or the speed of the object is faster than the speed of the wave:

Incidentally, although we implied that it is necessary to have a source of sound, it turns out, very interestingly, that once the object is moving faster than the speed of sound, it will make sound. That is, it is not necessary that it have a certain tone vibrational character. Any object moving through a medium faster than the speed at which the medium carries waves will generate waves on each side, automatically, just from the motion itself. This is simple in the case of sound, but it also occurs in the case of light. At first one might think nothing can move faster than the speed of light. However, light in glass has a phase velocity less than the speed of light in a vacuum, and it is possible to shoot a charged particle of very high energy through a block of glass such that the particle velocity is close to the speed of light in a vacuum, while the speed of light in the glass may be only 23 the speed of light in the vacuum. A particle moving faster than the speed of light in the medium will produce a conical wave of light with its apex at the source, like the wave wake from a boat (which is from the same effect, as a matter of fact). By measuring the cone angle, we can determine the speed of the particle. This is used technically to determine the speeds of particles as one of the methods of determining their energy in high-energy research. The direction of the light is all that needs to be measured.
This light is sometimes called Cherenkov radiation, because it was first observed by Cherenkov. How intense this light should be was analyzed theoretically by Frank and Tamm. The 1958 Nobel Prize for physics was awarded jointly to all three for this work.
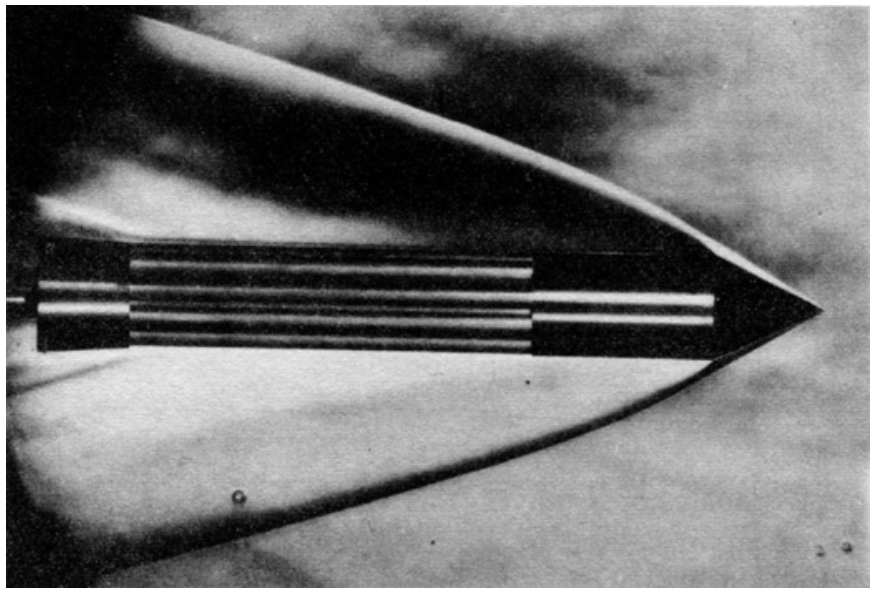
Fig. 51–2. A shock wave induced in a gas by a projectile moving faster than sound.
The corresponding circumstances in the case of sound are illustrated in Fig. 51–2, which is a photograph of an object moving through a gas at a speed greater than the speed of sound. The changes in pressure produce a change in refractive index, and with a suitable optical system the edges of the waves can be made visible. We see that the object moving faster than the speed of sound does, indeed, produce a conical wave. But closer inspection reveals that the surface is actually curved.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















