
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Symmetry and conservation laws
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 52
2024-07-15
1328
The symmetries of the physical laws are very interesting at this level, but they turn out, in the end, to be even more interesting and exciting when we come to quantum mechanics. For a reason which we cannot make clear at the level of the present discussion—a fact that most physicists still find somewhat staggering, a most profound and beautiful thing, is that, in quantum mechanics, for each of the rules of symmetry there is a corresponding conservation law; there is a definite connection between the laws of conservation and the symmetries of physical laws. We can only state this at present, without any attempt at explanation.
The fact, for example, that the laws are symmetrical for translation in space when we add the principles of quantum mechanics, turns out to mean that momentum is conserved.
That the laws are symmetrical under translation in time means, in quantum mechanics, that energy is conserved.
Invariance under rotation through a fixed angle in space corresponds to the conservation of angular momentum. These connections are very interesting and beautiful things, among the most beautiful and profound things in physics.
Incidentally, there are a number of symmetries which appear in quantum mechanics which have no classical analog, which have no method of description in classical physics. One of these is as follows: If ψ is the amplitude for some process or other, we know that the absolute square of ψ is the probability that the process will occur. Now if someone else were to make his calculations, not with this ψ, but with a ψ′ which differs merely by a change in phase (let Δ be some constant, and multiply eiΔ times the old ψ), the absolute square of ψ′, which is the probability of the event, is then equal to the absolute square of ψ:
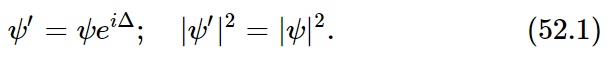
Therefore the physical laws are unchanged if the phase of the wave function is shifted by an arbitrary constant. That is another symmetry. Physical laws must be of such a nature that a shift in the quantum-mechanical phase makes no difference. As we have just mentioned, in quantum mechanics there is a conservation law for every symmetry. The conservation law which is connected with the quantum-mechanical phase seems to be the conservation of electrical charge. This is altogether a very interesting business!
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















