Vector line integrals
المؤلف:
Richard Fitzpatrick
المصدر:
Classical Electromagnetism
الجزء والصفحة:
p 23
13-7-2017
2590
A vector field is defined as a set of vectors associated with each point in space. For instance, the velocity v(r) in a moving liquid (e.g., a whirlpool) constitutes a vector field. By analogy, a scalar field is a set of scalars associated with each point in space. An example of a scalar field is the temperature distribution T(r) in a furnace. Consider a general vector field A(r). Let dl = (dx, dy, dz) be the vector element of line length. Vector line integrals often arise as
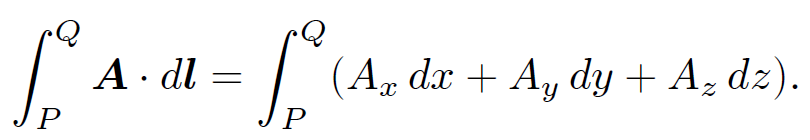(1.1)
For instance, if A is a force then the line integral is the work done in going from P to Q. As an example, consider the work done in a repulsive, inverse square law, central field F = -r/|r3|. The element of work done is dW = F . dl. Take P = (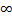
, 0, 0) and Q = (a, 0, 0). Route 1 is along the x-axis, so
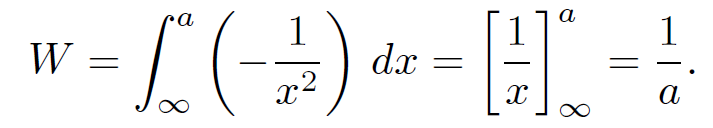(1.2)
The second route is, firstly, around a large circle (r = constant) to the point (a, 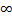, 0) and then parallel to the y-axis. In the first part no work is done since F is perpendicular to dl. In the second part
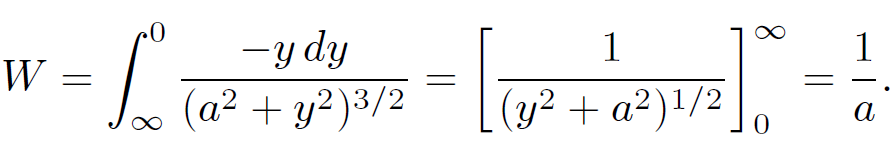(1.3)
In this case the integral is independent of path (which is just as well!).
الاكثر قراءة في الفيزياء العامة
اخر الاخبار
اخبار العتبة العباسية المقدسة
