
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The failure of classical physics
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 40
2024-05-23
2127
So, all in all, we might say that we have some difficulty. We might try some force law other than a spring, but it turns out that anything else will only make U higher. If we include more forms of energy, γ approaches unity more closely, contradicting the facts. All the classical theoretical things that one can think of will only make it worse. The fact is that there are electrons in each atom, and we know from their spectra that there are internal motions; each of the electrons should have at least 1/2 kT of kinetic energy, and something for the potential energy, so when these are added in, γ gets still smaller. It is ridiculous. It is wrong.
The first great paper on the dynamical theory of gases was by Maxwell in 1859. On the basis of ideas we have been discussing, he was able accurately to explain a great many known relations, such as Boyle’s law, the diffusion theory, the viscosity of gases, and things we shall talk about in the next chapter. He listed all these great successes in a final summary, and at the end he said, “Finally, by establishing a necessary relation between the motions of translation and rotation (he is talking about the 1/2 kT theorem) of all particles not spherical, we proved that a system of such particles could not possibly satisfy the known relation between the two specific heats.” He is referring to γ (which we shall see later is related to two ways of measuring specific heat), and he says we know we cannot get the right answer.
Ten years later, in a lecture, he said, “I have now put before you what I consider to be the greatest difficulty yet encountered by the molecular theory.” These words represent the first discovery that the laws of classical physics were wrong. This was the first indication that there was something fundamentally impossible, because a rigorously proved theorem did not agree with experiment. About 1905, Sir James Hopwood Jeans and Lord Rayleigh (John William Strutt) were to talk about this puzzle again. One often hears it said that physicists at the latter part of the nineteenth century thought they knew all the significant physical laws and that all they had to do was to calculate more decimal places. Someone may have said that once, and others copied it. But a thorough reading of the literature of the time shows they were all worrying about something. Jeans said about this puzzle that it is a very mysterious phenomenon, and it seems as though as the temperature falls, certain kinds of motions “freeze out.”
If we could assume that the vibrational motion, say, did not exist at low temperature and did exist at high temperature, then we could imagine that a gas might exist at a temperature sufficiently low that vibrational motion does not occur, so γ=1.40, or a higher temperature at which it begins to come in, so γ falls. The same might be argued for the rotation. If we can eliminate the rotation, say it “freezes out” at sufficiently low temperature, then we can understand the fact that the γ of hydrogen approaches 1.66 as we go down in temperature. How can we understand such a phenomenon? Of course, that these motions “freeze out” cannot be understood by classical mechanics. It was only understood when quantum mechanics was discovered.
Without proof, we may state the results for statistical mechanics of the quantum-mechanical theory. We recall that according to quantum mechanics, a system which is bound by a potential, for the vibrations, for example, will have a discrete set of energy levels, i.e., states of different energy. Now the question is: how is statistical mechanics to be modified according to quantum-mechanical theory? It turns out, interestingly enough, that although most problems are more difficult in quantum mechanics than in classical mechanics, problems in statistical mechanics are much easier in quantum theory! The simple result we have in classical mechanics, that n=n0e−energy/kT, becomes the following very important theorem: If the energies of the set of molecular states are called, say, E0, E1, E2, …, Ei, …, then in thermal equilibrium the probability of finding a molecule in the particular state of having energy Ei is proportional to e−Ei/kT. That gives the probability of being in various states. In other words, the relative chance, the probability, of being in state E1 relative to the chance of being in state E0, is
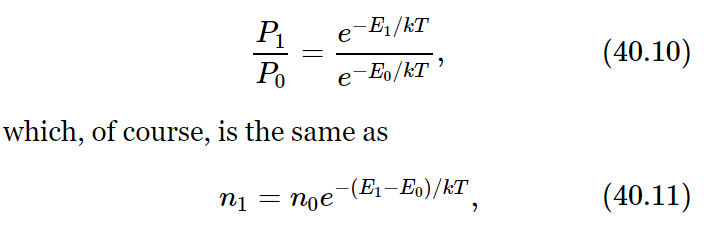
since P1=n1/N and P0=n0/N. So it is less likely to be in a higher energy state than in a lower one. The ratio of the number of atoms in the upper state to the number in the lower state is e raised to the power (minus the energy difference, over kT)—a very simple proposition.
Now it turns out that for a harmonic oscillator the energy levels are evenly spaced. Calling the lowest energy E0=0 (it actually is not zero, it is a little different, but it does not matter if we shift all energies by a constant), the first one is then E1=ℏω, and the second one is 2ℏω, and the third one is 3ℏω, and so on.
Now let us see what happens. We suppose we are studying the vibrations of a diatomic molecule, which we approximate as a harmonic oscillator. Let us ask what is the relative chance of finding a molecule in state E1 instead of in state E0. The answer is that the chance of finding it in state E1, relative to that of finding it in state E0, goes down as e−ℏω/kT. Now suppose that kT is much less than ℏω, and we have a low-temperature circumstance. Then the probability of its being in state E1 is extremely small. Practically all the atoms are in state E0. If we change the temperature but still keep it very small, then the chance of its being in state E1=ℏω remains infinitesimal—the energy of the oscillator remains nearly zero; it does not change with temperature so long as the temperature is much less than ℏω. All oscillators are in the bottom state, and their motion is effectively “frozen”; there is no contribution of it to the specific heat. We can judge, then, from Table 40–1, that at 100∘C, which is 373 degrees absolute, kT is much less than the vibrational energy in the oxygen or hydrogen molecules, but not so in the iodine molecule. The reason for the difference is that an iodine atom is very heavy, compared with hydrogen, and although the forces may be comparable in iodine and hydrogen, the iodine molecule is so heavy that the natural frequency of vibration is very low compared with the natural frequency of hydrogen. With ℏω higher than kT at room temperature for hydrogen, but lower for iodine, only the latter, iodine, exhibits the classical vibrational energy. As we increase the temperature of a gas, starting from a very low value of T, with the molecules almost all in their lowest state, they gradually begin to have an appreciable probability to be in the second state, and then in the next state, and so on. When the probability is appreciable for many states, the behavior of the gas approaches that given by classical physics, because the quantized states become nearly indistinguishable from a continuum of energies, and the system can have almost any energy. Thus, as the temperature rises, we should again get the results of classical physics, as indeed seems to be the case in Fig. 40–6. It is possible to show in the same way that the rotational states of atoms are also quantized, but the states are so much closer together that in ordinary circumstances kT is bigger than the spacing. Then many levels are excited, and the rotational kinetic energy in the system participates in the classical way. The one example where this is not quite true at room temperature is for hydrogen.
This is the first time that we have really deduced, by comparison with experiment, that there was something wrong with classical physics, and we have looked for a resolution of the difficulty in quantum mechanics in much the same way as it was done originally. It took 30 or 40 years before the next difficulty was discovered, and that had to do again with statistical mechanics, but this time the mechanics of a photon gas. That problem was solved by Planck, in the early years of the 20th century.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















