
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
!Parity is not conserved
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 52
2024-07-16
1461
It turns out that the laws of gravitation, the laws of electricity and magnetism, nuclear forces, all satisfy the principle of reflection symmetry, so these laws, or anything derived from them, cannot be used. But associated with the many particles that are found in nature there is a phenomenon called beta decay, or weak decay. One of the examples of weak decay, in connection with a particle discovered in about 1954, posed a strange puzzle. There was a certain charged particle which disintegrated into three π-mesons, as shown schematically in Fig. 52–5. This particle was called, for a while, a τ-meson. Now in Fig. 52–5 we also see another particle which disintegrates into two mesons; one must be neutral, from the conservation of charge. This particle was called a θ-meson. So on the one hand we have a particle called a τ, which disintegrates into three π-mesons, and a θ, which disintegrates into two π-mesons. Now it was soon discovered that the τ and the θ are almost equal in mass; in fact, within the experimental error, they are equal. Next, the length of time it took for them to disintegrate into three π’s and two π’s was found to be almost exactly the same; they live the same length of time. Next, whenever they were made, they were made in the same proportions, say, 14 percent τ’s to 86 percent θ’s.
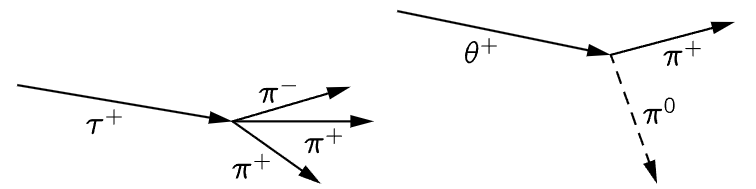
Fig. 52–5. A schematic diagram of the disintegration of a τ+ and a θ+ particle.
Anyone in his right mind realizes immediately that they must be the same particle, that we merely produce an object which has two different ways of disintegrating—not two different particles. This object that can disintegrate in two different ways has, therefore, the same lifetime and the same production ratio (because this is simply the ratio of the odds with which it disintegrates into these two kinds).
However, it was possible to prove (and we cannot here explain at all how), from the principle of reflection symmetry in quantum mechanics, that it was impossible to have these both come from the same particle—the same particle could not disintegrate in both of these ways. The conservation law corresponding to the principle of reflection symmetry is something which has no classical analog, and so this kind of quantum-mechanical conservation was called the conservation of parity. So, it was a result of the conservation of parity or, more precisely, from the symmetry of the quantum-mechanical equations of the weak decays under reflection, that the same particle could not go into both, so it must be some kind of coincidence of masses, lifetimes, and so on. But the more it was studied, the more remarkable the coincidence, and the suspicion gradually grew that possibly the deep law of the reflection symmetry of nature may be false.
As a result of this apparent failure, the physicists Lee and Yang suggested that other experiments be done in related decays to try to test whether the law was correct in other cases. The first such experiment was carried out by Miss Wu from Columbia, and was done as follows. Using a very strong magnet at a very low temperature, it turns out that a certain isotope of cobalt, which disintegrates by emitting an electron, is magnetic, and if the temperature is low enough that the thermal oscillations do not jiggle the atomic magnets about too much, they line up in the magnetic field. So the cobalt atoms will all line up in this strong field. They then disintegrate, emitting an electron, and it was discovered that when the atoms were lined up in a field whose B vector points upward, most of the electrons were emitted in a downward direction.
If one is not really “hep” to the world, such a remark does not sound like anything of significance, but if one appreciates the problems and interesting things in the world, then he sees that it is a most dramatic discovery: When we put cobalt atoms in an extremely strong magnetic field, more disintegration electrons go down than up. Therefore, if we were to put it in a corresponding experiment in a “mirror,” in which the cobalt atoms would be lined up in the opposite direction, they would spit their electrons up, not down; the action is unsymmetrical. The magnet has grown hairs! The south pole of a magnet is of such a kind that the electrons in a β-disintegration tend to go away from it; that distinguishes, in a physical way, the north pole from the south pole.
After this, a lot of other experiments were done: the disintegration of the π into μ and ν; μ into an electron and two neutrinos; nowadays, the Λ into proton and π; disintegration of Σ’s; and many other disintegrations. In fact, in almost all cases where it could be expected, all have been found not to obey reflection symmetry! Fundamentally, the law of reflection symmetry, at this level in physics, is incorrect.
In short, we can tell a Martian where to put the heart: we say, “Listen, build yourself a magnet, and put the coils in, and put the current on, and then take some cobalt and lower the temperature. Arrange the experiment so the electrons go from the foot to the head, then the direction in which the current goes through the coils is the direction that goes in on what we call the right and comes out on the left.” So it is possible to define right and left, now, by doing an experiment of this kind.
There are a lot of other features that were predicted. For example, it turns out that the spin, the angular momentum, of the cobalt nucleus before disintegration is 5 units of ℏ, and after disintegration it is 4 units. The electron carries spin angular momentum, and there is also a neutrino involved. It is easy to see from this that the electron must carry its spin angular momentum aligned along its direction of motion, the neutrino likewise. So it looks as though the electron is spinning to the left, and that was also checked. In fact, it was checked right here at Caltech by Boehm and Wapstra, that the electrons spin mostly to the left. (There were some other experiments that gave the opposite answer, but they were wrong!)
The next problem, of course, was to find the law of the failure of parity conservation. What is the rule that tells us how strong the failure is going to be? The rule is this: it occurs only in these very slow reactions, called weak decays, and when it occurs, the rule is that the particles which carry spin, like the electron, neutrino, and so on, come out with a spin tending to the left. That is a lopsided rule; it connects a polar vector velocity and an axial vector angular momentum, and says that the angular momentum is more likely to be opposite to the velocity than along it.
Now that is the rule, but today we do not really understand the whys and wherefores of it. Why is this the right rule, what is the fundamental reason for it, and how is it connected to anything else? At the moment we have been so shocked by the fact that this thing is unsymmetrical that we have not been able to recover enough to understand what it means with regard to all the other rules. However, the subject is interesting, modern, and still unsolved, so it seems appropriate that we discuss some of the questions associated with it.
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















