المركبات المتعامدة للمتجهات

بالرغم من أن الطريقة البيانية لجمع المنتجات بسيطة ومباشرة فإنها مرهقة وتعتمد دقتها على دقة الرسم فقط ، ولذلك فإننا نحتاج إلى طريقة أخرى خالية من هه العيوب. هذه الطريقة تسمى طريقة المركبات المتعامدة لجمع المتجهات. وقبل البدء , في وصف هذه الطريقة علينا أن نتعلم أولاً كيفية إيجاد المتعامدة.

لنفرض أن شخصاً ينتقل من النقطة A إلى النقطة C تقع على بعد 20 km  شمال شرق  A. السهم الموجه الذي يمثل هذه الإزاحة هو السهم الممتد من A إلى C في الشكل (1). من الممكن أيضاً الانتقال من A  إلى C بإتباع المسار ABC ، بمعنى ان نقوم أولاً بإزاحة من A  إلىB  ثم بإزاحة اخرى من B إلى C. النتيجة النهائية واحدة في الحالتين وهي أنك تنتقل من A  إلى C. ومن ثم يمكن استبدال الإزاحة من A  إلى C بالمتجهين AB و BC المتعامدين أحدهما على الآخر. هذان المتجهان يسميان المركبتين المتعامدتين للمتجه الأصلي. وسوف نرى ف القسم التالي أن المتجهات يمكن جمعها بسهولة باستخدام مركباتها المتعامدة. ولكننا يجب ان نتعلم أولاً كيف نستخدم علم حساب المثلثات لإيجاد هذه المركبات المتعامدة.

(1)

وبدلالة أضلاع المثلث قائم الزاوية الموضح بالشكل(2) ، يمكن تعريف هذه النسب المثلثية كما يلي :

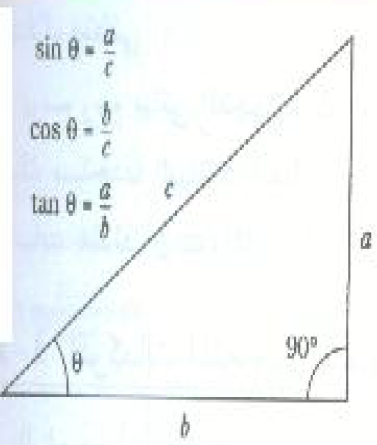
(2)

((1

هذا وتعطى معظم الآلات الحاسبة هذه الدوال لمختلف الزوايا. لاحظ أن الدوال المثلثية نسب لا بعدية. وهكذا يتضح من المعادلات (1) أنه يمكن إيجاد ضلعي المثلث بمعلومية الوتر c وإحدى الزاويتين :

θ            b = c  cos θ a = c  sin

لنحاول الآن تطبيق هذه المعلومة لإيجاد مركبتي متجه.

يمثل الشكل 3)) متجه إزاحة مقداره 20 cm  ويصنع زاوية قدرها 37^o مع المحور x. (سنستخدم الآن الاتجاهين x و y بدلاً من الشرق والشمال ، وإذا أردت يمكنك اعتبار أن x يمثل اتجاه الشرق و y اتجاه الشمال) . وطبقاً لما سبق يمكن القول أن المتجه الأصلي c يكافئ المجموع الاتجاهي لمركبتين c_x و c_y اللتين يمكن إيجاد مقداريهما باستخدام علاقتي الجيب وجيب التمام :

c_x= c cos 37^o = (20 cm)(0.80) = 16 cm               

c_y = c sin 37^o = (20 cm) (0.60) = 12 cm               

أي ان الإزاحة 20 cm التي تصنع زاوية قدرها 37^o  مع المحور x تكافئ مجموع المركبتين المتعامدتين c_x = 16 cm  في الاتجاه الموجب للمحورx و c_y = 12 cm  في الاتجاه السالب للمحورy.

(3)

هذه الطريقة يمكن استخدامها لاستبدلا أي متجه بمركباته المتعامدة ، فإذا ما تعلمت كيف تفعل ذلك سيكون من  السهل عليك جمع ( أو طرح) أي نوع من المتجهات. ولكن قبل متابعة الموضوع عليك ان تتأكد أنك تستطيع إيجاد المركبتين x، y للمتجهات المبينة بالشكل(4) لاحظ ان اتجاه كل مركبة يبين بإشارة جبرية مناسبة. فعندما تكتبc_x = 15 mm  فهذا يعني أن المركبة في الاتجاه السالب للمحور x. وبالمثل فإن c_y = 30 mm تعنى ان المركبة تشير في الاتجاه الموجب للمحور y. أي ان أتجاه مركبة المتجه يعطي كإشارة جبرية ملحقة بقيمتها العددية.