


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-6-2021
Date: 20-6-2021
Date: 5-6-2021
|
A differential 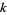 -form is a tensor of tensor rank
-form is a tensor of tensor rank 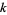 that is antisymmetric under exchange of any pair of indices. The number of algebraically independent components in
that is antisymmetric under exchange of any pair of indices. The number of algebraically independent components in 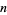 dimensions is given by the binomial coefficient
dimensions is given by the binomial coefficient 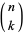 . In particular, a one-form
. In particular, a one-form 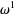 (often simply called a "differential") is a quantity
(often simply called a "differential") is a quantity
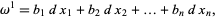 |
(1) |
where 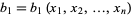 , ...,
, ..., 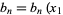 ,
, 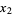 , ...,
, ..., 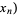 are the components of a covariant tensor. Changing variables from
are the components of a covariant tensor. Changing variables from  to
to 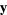 gives
gives
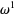 |
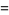 |
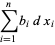 |
(2) |
 |
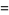 |
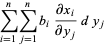 |
(3) |
 |
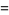 |
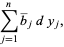 |
(4) |
where
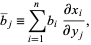 |
(5) |
which is the covariant transformation law.
A 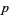 -alternating multilinear form on a vector space
-alternating multilinear form on a vector space 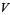 corresponds to an element of
corresponds to an element of 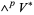 , the
, the 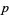 th exterior power of the dual vector space to
th exterior power of the dual vector space to 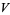 . A differential
. A differential 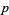 -form on a manifold is a bundle section of the vector bundle
-form on a manifold is a bundle section of the vector bundle 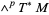 , the
, the 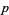 th exterior power of the cotangent bundle. Hence, it is possible to write a
th exterior power of the cotangent bundle. Hence, it is possible to write a 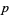 -form in coordinates by
-form in coordinates by
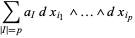 |
(6) |
where 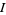 ranges over all increasing subsets of
ranges over all increasing subsets of 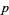 elements from
elements from 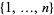 , and the
, and the 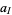 are functions.
are functions.
An important operation on differential forms, the exterior derivative, is used in the celebrated Stokes' theorem. The exterior derivative 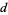 of a
of a 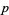 form is a
form is a 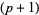 -form. In fact, by definition, if
-form. In fact, by definition, if 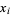 is the coordinate function, thought of as a zero-form, then
is the coordinate function, thought of as a zero-form, then 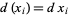 .
.
Another important operation on forms is the wedge product, or exterior product. If 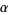 is a
is a 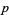 -form and
-form and 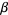 is
is 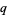 -form, then
-form, then 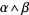 is a
is a 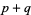 form. Also, a
form. Also, a 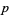 -form can be contracted with an
-form can be contracted with an 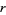 -vector, i.e., a bundle section of
-vector, i.e., a bundle section of 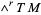 , to give a
, to give a 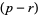 -form, or if
-form, or if 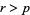 , an
, an 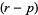 -vector. If the manifold has a metric, then there is an operation dual to the exterior product, called the interior product.
-vector. If the manifold has a metric, then there is an operation dual to the exterior product, called the interior product.
In higher dimensions, there are more kinds of differential forms. For instance, on the tangent space to 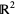 there is the zero-form 1, two one-forms
there is the zero-form 1, two one-forms 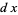 and
and 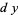 , and one two-form
, and one two-form 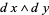 . A one-form can be written uniquely as
. A one-form can be written uniquely as 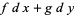 . In four dimensions,
. In four dimensions, 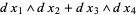 is a two-form that cannot be written as
is a two-form that cannot be written as 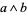 .
.
The minimum number of terms necessary to write a form is sometimes called the rank of the form, usually in the case of a two-form. When a form has rank one, it is called decomposable. Another meaning for rank of a form is its rank as a tensor, in which case a 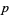 -form can be described as an antisymmetric tensor of rank
-form can be described as an antisymmetric tensor of rank 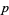 , in fact of type
, in fact of type 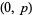 . The rank of a form can also mean the dimension of its form envelope, in which case the rank is an integer-valued function. With the latter definition of rank, a
. The rank of a form can also mean the dimension of its form envelope, in which case the rank is an integer-valued function. With the latter definition of rank, a 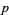 -form is decomposable iff it has rank
-form is decomposable iff it has rank 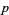 .
.
When 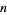 is the dimension of a manifold
is the dimension of a manifold 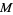 , then
, then 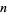 is also the dimension of the tangent space
is also the dimension of the tangent space 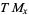 . Consequently, an
. Consequently, an 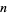 -form always has rank one, and for
-form always has rank one, and for 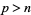 , a
, a 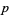 -form must be zero. Hence, an
-form must be zero. Hence, an 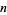 -form is called a top-dimensional form. A top-dimensional form can be form-integrated without using a metric. Consequently, a
-form is called a top-dimensional form. A top-dimensional form can be form-integrated without using a metric. Consequently, a 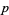 -form can be integrated on a
-form can be integrated on a 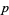 -dimensional submanifold. Differential forms are a vector space (with a C-infty topology) and therefore have a dual space. Submanifolds represent an element of the dual via integration, so it is common to say that they are in the dual space of forms, which is the space of currents. With a metric, the Hodge star operator
-dimensional submanifold. Differential forms are a vector space (with a C-infty topology) and therefore have a dual space. Submanifolds represent an element of the dual via integration, so it is common to say that they are in the dual space of forms, which is the space of currents. With a metric, the Hodge star operator 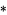 defines a map from
defines a map from 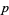 -forms to
-forms to 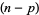 -forms such that
-forms such that 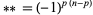 .
.
When 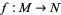 is a smooth map, it pushes forward manifold tangent vectors from
is a smooth map, it pushes forward manifold tangent vectors from 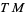 to
to 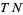 according to the Jacobian
according to the Jacobian 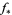 . Hence, a differential form on
. Hence, a differential form on 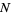 pulls back to a differential form on
pulls back to a differential form on 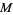 .
.
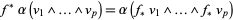 |
(7) |
The pullback map is a linear map which commutes with the exterior derivative,
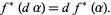 |



|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
معهد القرآن الكريم النسوي يقدم خدماته لزائري الإمام الكاظم (عليه السلام)
|
|
|