The separation of variables
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
322
2025-11-24
52
The separation of variables
Physical intuition suggests that the full Schrödinger equation ought to separate into two equations, one for the motion of the atom as a whole through space and the other for the motion of the electron relative to the nucleus. We show in Further information 10.1 how this separation is achieved, and that the Schrödinger equation for the internal motion of the electron relative to the nucleus is
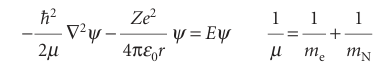
where differentiation is now with respect to the coordinates of the electron relative to the nucleus. The quantity µ is called the reduced mass. The reduced mass is very similar to the electron mass because mN, the mass of the nucleus, is much larger than the mass of an electron, so 1/µ ≈ 1/me. In all except the most precise work, the reduced mass can be replaced by me. Because the potential energy is centrosymmetric (independent of angle), we can suspect that the equation is separable into radial and angular components. Therefore, we write
ψ(r,θ,φ) = R(r)Y(θ, φ)
and examine whether the Schrödinger equation can be separated into two equations, one for R and the other for Y. As shown in Further information 10.1, the equation does separate, and the equations we have to solve are
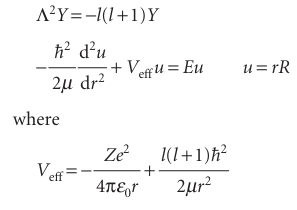
Equation 10.8 is the same as the Schrödinger equation for a particle free to move round a central point, and we considered it in Section 9.7. The solutions are the spherical harmonics (Table 9.3), and are specified by the quantum numbers l and ml. We consider them in more detail shortly. Equation 10.9 is called the radial wave equation. The radial wave equation is the description of the motion of a particle of mass µin a one-dimensional region 0 ≤ r<∞where the potential energy is V eff.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
