The Pauli principle
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص337- 339
2025-11-25
48
The Pauli principle
Lithium, with Z = 3, has three electrons. The first two occupy a 1s orbital drawn even more closely than in He around the more highly charged nucleus. The third electron, however, does not join the first two in the 1s orbital because that configuration is for bidden by the Pauli exclusion principle: No more than two electrons may occupy any given orbital, and if two do occupy one orbital, then their spins must be paired. Electrons with paired spins, denoted ↑↓, have zero net spin angular momentum because the spin of one electron is cancelled by the spin of the other. Specifically, one electron has ms =+1–2, the other has ms =−1/2 and they are orientated on their respective cones so that the resultant spin is zero (Fig. 10.18). The exclusion principle is the key to the structure of complex atoms, to chemical periodicity, and to molecular structure. It was proposed by Wolfgang Pauli in 1924 when he was trying to account for the absence of some lines in the spectrum of helium. Later he was able to derive a very general form of the principle from theoretical considerations. The Pauli exclusion principle in fact applies to any pair of identical fermions (particles with half integral spin).
Thus it applies to protons, neutrons, and 13C nuclei (all of which have spin 1/2) and to 35Cl nuclei (which have spin 3/2). It does not apply to identical bosons (particles with integral spin), which include photons (spin 1), 12C nuclei (spin 0). Any number of identical bosons may occupy the same state (that is, be described by the same wavefunction).
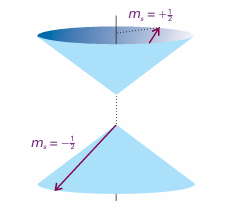
Fig. 10.18 Electrons with paired spins have zero resultant spin angular momentum. They can be represented by two vectors that lie at an indeterminate position on the cones shown here, but wherever one lies on its cone, the other points in the opposite direction; their resultant is zero.
The Pauli exclusion principle is a special case of a general statement called the Pauli principle: When the labels of any two identical fermions are exchanged, the total wavefunction changes sign; when the labels of any two identical bosons are exchanged, the total wavefunction retains the same sign. By ‘total wavefunction’ is meant the entire wavefunction, including the spin of the particles. To see that the Pauli principle implies the Pauli exclusion principle, we consider the wavefunction for two electrons ψ(1,2). The Pauli principle implies that it is a fact of nature (which has its roots in the theory of relativity) that the wavefunction must change sign if we interchange the labels 1 and 2 wherever they occur in the function:
ψ(2,1) =−ψ(1,2)
Suppose the two electrons in an atom occupy an orbital ψ, then in the orbital approximation the overall wavefunction is ψ(1)ψ(2). To apply the Pauli principle, we must deal with the total wavefunction, the wavefunction including spin. There are several possibilities for two spins: both α, denoted α(1)α(2), both β, denoted β(1)β(2), and oneαthe other β, denoted either α(1)β(2) or α(2)β(1). Because we cannot tell which electron is α and which is β, in the last case it is appropriate to express the spin states as the (normalized) linear combinations
σ+(1,2) = (1/21/2) {α (1)β(2) + β (1)α(2)}
σ−(1,2) = (1/21/2) {α (1)β(2) − β(1)α(2)}
because these combinations allow one spin to be α and the other β with equal prob ability. The total wavefunction of the system is therefore the product of the orbital part and one of the four spin states:
ψ(1)ψ(2)α(1)α(2) ψ(1)ψ(2)β(1)β(2) ψ(1)ψ(2)σ+(1,2) ψ(1)ψ(2)σ−(1,2)
The Pauli principle says that for a wavefunction to be acceptable (for electrons), it must change sign when the electrons are exchanged. In each case, exchanging the labels 1 and 2 converts the factor ψ (1)ψ(2) into ψ (2)ψ(1), which is the same, because the order of multiplying the functions does not change the value of the product. The same is true of α (1)α(2) and β(1)β(2). Therefore, the first two overall products are not allowed, because they do not change sign. The combination σ+(1,2) changes to
σ+(2,1) = (1/21/2){α(2)β(1) + β(2)α(1)} = σ+(1,2)
because it is simply the original function written in a different order. The third over all product is therefore also disallowed. Finally, consider σ−(1,2):
σ−(2,1) = (1/21/2){α(2)β(1) − β(2)α(1)} =−(1/21/2){α(1)β(2) − β(1)α(2)} =−σ−(1,2)
This combination does change sign (it is ‘antisymmetric’). The product ψ(1)ψ(2) σ−(1,2) also changes sign under particle exchange, and therefore it is acceptable.
Now we see that only one of the four possible states is allowed by the Pauli prin ciple, and the one that survives has paired αandβspins. This is the content of the Pauli exclusion principle. The exclusion principle is irrelevant when the orbitals occupied by the electrons are different, and both electrons may then have (but need not have) the same spin state. Nevertheless, even then the overall wavefunction must still be antisymmetric overall, and must still satisfy the Pauli principle itself. A final point in this connection is that the acceptable product wavefunction ψ(1)ψ(2)σ−(1,2) can be expressed as a determinant:
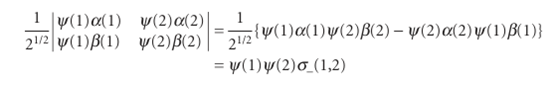
Any acceptable wavefunction for a closed-shell species can be expressed as a Slater determinant, as such determinants are known. In general, for Nelectrons in orbitals ψa,ψb, . . .
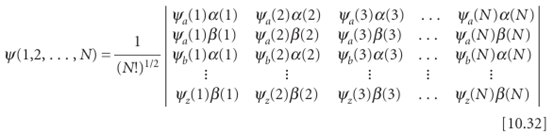
Writing a many-electron wavefunction in this way ensures that it is antisymmetric under the interchange of any pair of electrons, as is explored in Problem 10.23. Now we can return to lithium. In Li (Z=3), the third electron cannot enter the 1s orbital because that orbital is already full: we say the Kshell is completeand that the two electrons form a closed shell. Because a similar closed shell is characteristic of the He atom, we denote it [He]. The third electron is excluded from the Kshell and must occupy the next available orbital, which is one with n=2 and hence belonging to the Lshell. However, we now have to decide whether the next available orbital is the 2s orbital or a 2porbital, and therefore whether the lowest energy configuration of the atom is [He]2s1or [He]2p1.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
