Radial distribution functions
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص331-332
2025-11-24
65
Radial distribution functions
The wavefunction tells us, through the value of |ψ|2, the probability of finding an electron in any region. We can imagine a probe with a volume dτ and sensitive to electrons, and which we can move around near the nucleus of a hydrogen atom. Because the probability density in the ground state of the atom is |ψ|2∝e−2Zr/a0, the reading from the detector decreases exponentially as the probe is moved out along any radius but is constant if the probe is moved on a circle of constant radius (Fig. 10.13). Now consider the probability of finding the electron anywhere between the two walls of a spherical shell of thickness drat a radius r. The sensitive volume of the probe is now the volume of the shell (Fig. 10.14), which is 4πr2dr (the product of its surface area, 4πr2, and its thickness, dr). The probability that the electron will be found between the inner and outer surfaces of this shell is the probability density at the radius r multiplied by the volume of the probe, or |ψ|2×4πr2dr. This expression has the form P(r)dr, where
P(r)=4πr2ψ2
The more general expression, which also applies to orbitals that are not spherically symmetrical, is
P(r)=r2R(r)2
Where R(r) is the radial wavefunction for the orbital in question.
Justification 10.2The general form of the radial distribution function the probability of finding an electron in a volume element dτ when its wavefunction is ψ=RYis|RY2 dτ with dτ=r2drsinθdθdφ. The total probability of finding the electron at any angle at a constant radius is the integral of this probability over the surface of a sphere of radius r, and is written P(r)dr; so
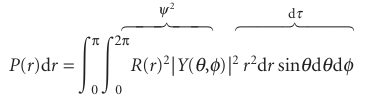
The last equality follows from the fact that the spherical harmonics are normalized to 1 (see Example 10.2). It follows that P(r)=r2R(r)2, as stated in the text.
The radial distribution function,P(r), is a probability density in the sense that, when it is multiplied by dr, it gives the probability of finding the electron anywhere between the two walls of a spherical shell of thickness drat the radius r. For a 1sorbital,
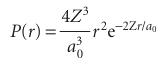
Let’s interpret this expression:
1Because r2=0 at the nucleus, at the nucleus P (0) =0.
2As r→∞,P(r)→0 on account of the exponential term.
3The increase in r2 and the decrease in the exponential factor means that P passes through a maximum at an intermediate radius (see Fig. 10.14).
The maximum of P(r), which can be found by differentiation, marks the most prob able radius at which the electron will be found, and for a 1sorbital in hydrogen occurs at r=a0, the Bohr radius. When we carry through the same calculation for the radial distribution function of the 2sorbital in hydrogen, we find that the most probable radius is 5.2a0=275 pm. This larger value reflects the expansion of the atom as its energy increases.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
