P Orbitals
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص332-334
2025-11-24
63
P Orbitals
The three 2p orbitals are distinguished by the three different values that ml can take when l=1. Because the quantum number ml tells us the orbital angular momentum around an axis, these different values of ml denote orbitals in which the electron has different orbital angular momenta around an arbitrary z-axis but the same magnitude of that momentum (because l is the same for all three). The orbital with ml=0, for instance, has zero angular momentum around the z-axis. Its angular variation is proportional to cos θ, so the probability density, which is proportional to cos2θ, has its maximum value on either side of the nucleus along the z-axis (at θ=0 and 180°). The wavefunction of a 2p-orbital with ml=0 is
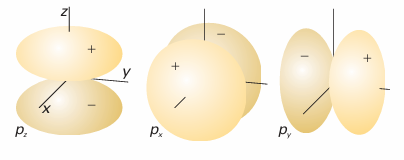
Fig. 10.15The boundary surfaces of porbitals. A nodal plane passes through the nucleus and separates the two lobes of each orbital. The dark and light areas denote regions of opposite sign of the wavefunction
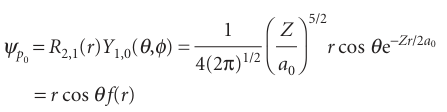
Where f(r) is a function only of r. Because in spherical polar coordinates z=r cos θ, this wavefunction may also be written
Ψ pz=zf(r)
All p orbitals with ml=0 have wavefunctions of this form regardless of the value of n. This way of writing the orbital is the origin of the name ‘pz orbital’: its boundary sur face is shown in Fig. 10.15. The wavefunction is zero everywhere in the xy-plane, where z=0, so the xy-plane is a nodal plane of the orbital: the wavefunction changes sign on going from one side of the plane to the other. The wavefunctions of 2porbitals with ml=±1 have the following form:
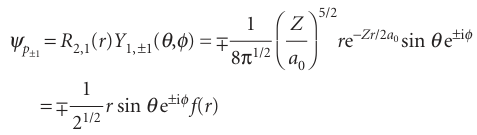
We saw in Chapter 8 that a moving particle can be described by a complex wavefunction. In the present case, the functions correspond to non-zero angular momentum about the z-axis: e+iφ corresponds to clockwise rotation when viewed from below, and e−iφ corresponds to counter-clockwise rotation (from the same viewpoint). They have zero amplitude where θ=0 and 180° (along the z-axis) and maximum amplitude at 90°, which is in the xy-plane. To draw the functions it is usual to represent them as standing waves. To do so, we take the real linear combinations
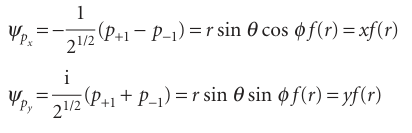
These linear combinations are indeed standing waves with no net orbital angular momentum around the z-axis, as they are superpositions of states with equal and opposite values of ml. The pxorbital has the same shape as a pzorbital, but it is directed along the x-axis (see Fig. 10.15); the py orbital is similarly directed along the y-axis. The wavefunction of any p orbital of a given shell can be written as a product of x, y, or z and the same radial function (which depends on the value of n).
Justification 10.3 The linear combination of degenerate wavefunctions We justify here the step of taking linear combinations of degenerate orbitals when we want to indicate a particular point. The freedom to do so rests on the fact that, whenever two or more wavefunctions correspond to the same energy, any linear combination of them is an equally valid solution of the Schrödinger equation. Suppose ψ1 and ψ2 are both solutions of the Schrödinger equation with energy E; then we know that
Hψ1=Eψ1 Hψ2=Eψ2
Now consider the linear combination
ψ=c1ψ1+c2ψ2
where c1 and c2 are arbitrary coefficients. Then it follows that Hψ=H(c1ψ1+c2ψ2)=c1Hψ1+c2Hψ2=c1Eψ1+c2Eψ2=Eψ Hence, the linear combination is also a solution corresponding to the same energy E.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
