
The building-up principle
 المؤلف:
Peter Atkins، Julio de Paula
المؤلف:
Peter Atkins، Julio de Paula
 المصدر:
ATKINS PHYSICAL CHEMISTRY
المصدر:
ATKINS PHYSICAL CHEMISTRY
 الجزء والصفحة:
ص340-342
الجزء والصفحة:
ص340-342
 2025-11-25
2025-11-25
 50
50
The building-up principle
The extension of this argument is called the building-up principle, or the Aufbau principle, from the German word for building up, which will be familiar from introductory courses. In brief, we imagine the bare nucleus of atomic number Z, and then feed into the orbitals Z electrons in succession. The order of occupation is , 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s , and each orbital may accommodate up to two electrons. As an example, consider the carbon atom, for which Z = 6 and there are six electrons to accommodate. Two electrons enter and fill the 1s orbital, two enter and fill the 2s orbital, leaving two electrons to occupy the orbitals of the 2p subshell. Hence the ground-state configuration of C is 1s2 2s2 2p2, or more succinctly [He]2s2 2p2, with [He] the helium-like 1s2 core. However, we can be more precise: we can expect the last two electrons to occupy different 2p orbitals because they will then be further apart on average and repel each other less than if they were in the same orbital. Thus, one electron can be thought of as occupying the 2px orbital and the other the 2py orbital (the x, y, z designation is arbitrary, and it would be equally valid to use the complex forms of these orbitals), and the lowest energy configuration of the atom is [He]2s2 2p1x 2p1y. The same rule applies whenever degenerate orbitals of a subshell are available for occupation. Thus, another rule of the building-up principle is: Electrons occupy different orbitals of a given subshell before doubly occupying any one of them.
For instance, nitrogen (Z = 7) has the configuration [He]2s2 2p1x 2p1y 2p1z, and only when we get to oxygen (Z = 8) is a 2p orbital doubly occupied, giving [He]2s2 2p2x 2p1y 2p1z. When electrons occupy orbitals singly, we invoke Hund’s maximum multiplicity rule: An atom in its ground state adopts a configuration with the greatest number of unpaired electrons.
The explanation of Hund’s rule is subtle, but it reflects the quantum mechanical property of spin correlation, that electrons with parallel spins behave as if they have a tendency to stay well apart, and hence repel each other less. In essence, the effect of spin correlation is to allow the atom to shrink slightly, so the electron–nucleus interaction is improved when the spins are parallel. We can now conclude that, in the ground state of the carbon atom, the two 2p electrons have the same spin, that all three 2p electrons in the N atoms have the same spin, and that the two 2p electrons in different orbitals in the O atom have the same spin (the two in the 2px orbital are necessarily paired).
Justification 10.6 Spin correlation Suppose electron 1 is described by a wavefunction ψa(r1) and electron 2 is described by a wavefunction ψb(r2); then, in the orbital approximation, the joint wavefunction of the electrons is the product ψ = ψa(r1)ψb(r2). However, this wavefunction is not acceptable, because it suggests that we know which electron is in which orbital, whereas we cannot keep track of electrons. According to quantum mechanics, the correct description is either of the two following wavefunctions:
ψ±= (1/2 1/2) {ψa(r1) ψb(r2) ± ψb(r1) ψa(r2)}
According to the Pauli principle, because ψ+ is symmetrical under particle inter change, it must be multiplied by an antisymmetric spin function (the one denoted σ−). That combination corresponds to a spin-paired state. Conversely, ψ− is anti-symmetric, so it must be multiplied by one of the three symmetric spin states. These three symmetric states correspond to electrons with parallel spins (see Section 10.7 for an explanation). Now consider the values of the two combinations when one electron approaches another, and r1 = r2. We see that ψ− vanishes, which means that there is zero prob ability of finding the two electrons at the same point in space when they have parallel spins. The other combination does not vanish when the two electrons are at the same point in space. Because the two electrons have different relative spatial distributions depending on whether their spins are parallel or not, it follows that their Coulombic interaction is different, and hence that the two states have different energies.
Neon, with Z = 10, has the configuration [He]2s22p6, which completes the L shell. This closed-shell configuration is denoted [Ne], and acts as a core for subsequent elements. The next electron must enter the 3s orbital and begin a new shell, so an Na atom, with Z = 11, has the configuration [Ne]3s1. Like lithium with the configuration [He]2s1, sodium has a single s electron outside a complete core. This analysis has brought us to the origin of chemical periodicity. The L shell is completed by eight electrons, so the element with Z = 3 (Li) should have similar properties to the element with Z=11 (Na). Likewise, Be (Z = 4) should be similar to Z = 12 (Mg), and so on, up to the noble gases He (Z = 2), Ne (Z = 10), and Ar (Z = 18).
Ten electrons can be accommodated in the five 3d orbitals, which accounts for the electron configurations of scandium to zinc. Calculations of the type discussed in Section 10.5 show that for these atoms the energies of the 3d orbitals are always lower than the energy of the 4s orbital. However, spectroscopic results show that Sc has the configuration [Ar]3d1 4s2, instead of [Ar]3d3 or [Ar]3d2 4s1. To understand this observation, we have to consider the nature of electron–electron repulsions in 3d and 4s orbitals. The most probable distance of a 3d electron from the nucleus is less than that for a 4s electron, so two 3d electrons repel each other more strongly than two 4s electrons. As a result, Sc has the configuration [Ar]3d14s2 rather than the two alternatives, for then the strong electron–electron repulsions in the 3d orbitals are minimized. The total energy of the atom is least despite the cost of allowing electrons to populate the high energy 4s orbital (Fig. 10.21). The effect just described is generally true for scandium through zinc, so their electron configurations are of the form [Ar]3dn4s2, where n = 1 for scandium and n = 10 for zinc. Two notable exceptions, which are observed experimentally, are Cr, with electron configuration [Ar]3d54s1, and Cu, with electron configuration [Ar]3d104s1(see Further reading for a discussion of the theoretical basis for these exceptions).
At gallium, the building-up principle is used in the same way as in preceding periods. Now the 4s and 4p subshells constitute the valence shell, and the period ter minates with krypton. Because 18 electrons have intervened since argon, this period is the first ‘long period’ of the periodic table. The existence of the d-block elements (the ‘transition metals’) reflects the stepwise occupation of the 3d orbitals, and the subtle shades of energy differences and effects of electron–electron repulsion along this series gives rise to the rich complexity of inorganic d-metal chemistry. A similar intrusion of the f orbitals in Periods 6 and 7 accounts for the existence of the f block of the periodic table (the lanthanoids and actinoids). We derive the configurations of cations of elements in the s, p, and d blocks of the periodic table by removing electrons from the ground-state configuration of the neutral atom in a specific order. First, we remove valence p electrons, then valence s electrons, and then as many d electrons as are necessary to achieve the specified charge. For instance, because the configuration of V is [Ar]3d3 4s2, the V2+ cation has the configuration [Ar]3d3. It is reasonable that we remove the more energetic 4s electrons in order to form the cation, but it is not obvious why the [Ar]3d3 configuration is pre ferred in V2+ over the [Ar]3d14s2 configuration, which is found in the isoelectronic Sc atom. Calculations show that the energy difference between [Ar]3d3 and [Ar]3d1 4s2 depends on Zeff. As Zeff increases, transfer of a 4s electron to a 3d orbital becomes more favourable because the electron–electron repulsions are compensated by attractive interactions between the nucleus and the electrons in the spatially compact 3d orbital. Indeed, calculations reveal that, for a sufficiently large Zeff, [Ar]3d3 is lower in energy than [Ar]3d1 4s2. This conclusion explains why V2+ has a [Ar]3d3 configuration and also accounts for the observed [Ar]4s0 3dn configurations of the M2+ cations of Sc through Zn.
The configurations of anions of the p-block elements are derived by continuing the building-up procedure and adding electrons to the neutral atom until the configuration of the next noble gas has been reached. Thus, the configuration of the O2− ion is achieved by adding two electrons to [He]2s2 2p4, giving [He]2s2 2p6, the same as the configuration of neon.
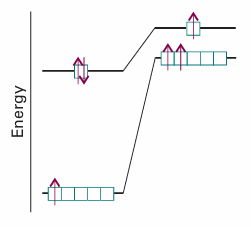
Fig. 10.21 Strong electron–electron repulsions in the 3d orbitals are minimized in the ground state of Sc if the atom has the configuration [Ar]3d1 4s2 (shown on the left) instead of [Ar]3d2 4s1 (shown on the right). The total energy of the atom is lower when it has the [Ar]3d1 4s2 configuration despite the cost of populating the high energy 4s orbital.
 الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


