Atomic orbitals
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص328-330
2025-11-24
70
Atomic orbitals
The orbital occupied in the ground state is the one with n = 1 (and therefore with l = 0 and ml = 0, the only possible values of these quantum numbers when n = 1). From Table 10.1 we can write (for Z = 1):
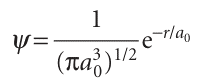
This wavefunction is independent of angle and has the same value at all points of constant radius; that is, the 1s orbital is spherically symmetrical. The wavefunction decays exponentially from a maximum value of 1/ (πa0 3)1/2 at the nucleus (at r = 0). It follows that the most probable point at which the electron will be found is at the nucleus itself.
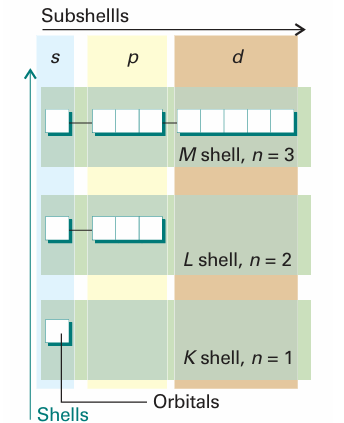
Fig. 10.8 The organization of orbitals (white squares) into subshells (characterized by l) and shells (characterized by n).
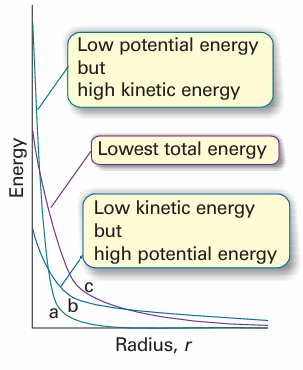
Fig. 10.9 The balance of kinetic and potential energies that accounts for the structure of the ground state of hydrogen (and similar atoms). (a) The sharply curved but localized orbital has high mean kinetic energy, but low mean potential energy; (b) the mean kinetic energy is low, but the potential energy is not very favourable; (c) the compromise of moderate kinetic energy and moderately favourable potential energy.
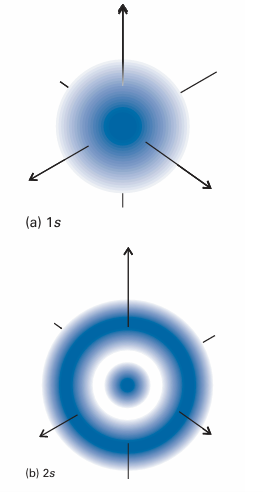
Fig. 10.10 Representations of the 1s and 2s hydrogenic atomic orbitals in terms of their electron densities (as represented by the density of shading)
We can understand the general form of the ground-state wavefunction by consid ering the contributions of the potential and kinetic energies to the total energy of the atom. The closer the electron is to the nucleus on average, the lower its average poten tial energy. This dependence suggests that the lowest potential energy should be obtained with a sharply peaked wavefunction that has a large amplitude at the nucleus and is zero everywhere else (Fig. 10.9). However, this shape implies a high kinetic energy, because such a wavefunction has a very high average curvature. The electron would have very low kinetic energy if its wavefunction had only a very low average curvature. However, such a wavefunction spreads to great distances from the nucleus and the average potential energy of the electron will be correspondingly high. The actual ground-state wavefunction is a compromise between these two extremes: the wavefunction spreads away from the nucleus (so the expectation value of the poten tial energy is not as low as in the first example, but nor is it very high) and has a reas onably low average curvature (so the expectation of the kinetic energy is not very low, but nor is it as high as in the first example). The energies of ns orbitals increase (become less negative; the electron becomes less tightly bound) as n increases because the average distance of the electron from the nucleus increases. By the virial theorem with b =−1 (eqn 9.35), EK =−1–2 V so, even though the average kinetic energy decreases as n increases, the total energy is equal to 1 2 V, which becomes less negative as n increases. One way of depicting the probability density of the electron is to represent |ψ |2 by the density of shading (Fig. 10.10). A simpler procedure is to show only the boundary surface, the surface that captures a high proportion (typically about 90 per cent) of the electron probability. For the 1s orbital, the boundary surface is a sphere centred on the nucleus (Fig. 10.11).
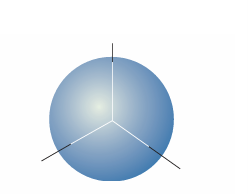
Fig. 10.11 The boundary surface of an s orbital, within which there is a 90 per cent probability of finding the electron.
The general expression for the mean radius of an orbital with quantum numbers l and n is
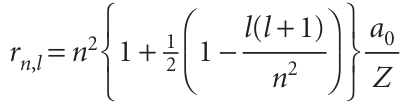
The variation with n and l is shown in Fig. 10.12. Note that, for a given principal quantum number, the mean radius decreases as l increases, so the average distance of an electron from the nucleus is less when it is in a 2porbital, for instance, than when it is in a 2sorbital.
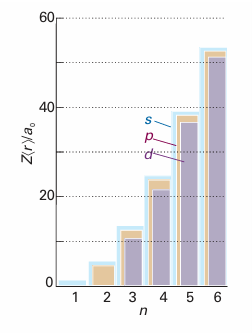
Fig. 10.12The variation of the mean radius of a hydrogenic atom with the principal and orbital angular momentum quantum numbers. Note that the mean radius lies in the order d<p
All s-orbitals are spherically symmetric, but differ in the number of radial nodes. For example, the 1s, 2s,and 3sorbitals have 0, 1, and 2 radial nodes, respectively. In general, an ns orbital has n−1 radial nodes.
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
