Ionization energies and electron affinities
المؤلف:
Peter Atkins، Julio de Paula
المصدر:
ATKINS PHYSICAL CHEMISTRY
الجزء والصفحة:
ص342-344
2025-11-25
41
Ionization energies and electron affinities
The minimum energy necessary to remove an electron from a many-electron atom in the gas phase is the first ionization energy, I1, of the element. The second ionization energy, I2, is the minimum energy needed to remove a second electron (from the singly charged cation). The variation of the first ionization energy through the periodic table is shown in Fig. 10.22 and some numerical values are given in Table 10.3. In thermodynamic calculations we often need the standard enthalpy of ionization, ∆ionH7. As shown in the Justification below, the two are related by
∆ionHo(T) = I + 5/2RT
At 298 K, the difference between the ionization enthalpy and the corresponding ionization energy is 6.20 kJ mol−1.
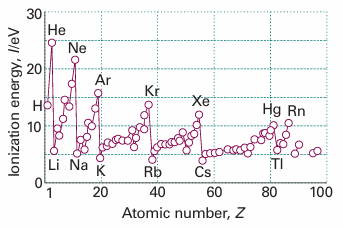
Fig. 10.22 The first ionization energies of the elements plotted against atomic number.
Justification 10.7 The ionization enthalpy and the ionization energy It follows from Kirchhoff’s law (Section 2.9 and eqn 2.36) that the reaction enthalpy for
M(g)→M+(g)+e−(g)
at a temperature T is related to the value at T = 0 by
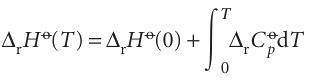
The molar constant-pressure heat capacity of each species in the reaction is 5/2R, so ∆rCop =+5/2R. The integral in this expression therefore evaluates to +5/2RT. The reaction enthalpy at T = 0 is the same as the (molar) ionization energy, I. Equation 10.33 then follows. The same expression applies to each successive ionization step, so the overall ionization enthalpy for the formation of M2+ is
∆rHo(T) =I1+I2+5RT
The electron affinity, Eea, is the energy released when an electron attaches to a gas phase atom (Table 10.4). In a common, logical, but not universal convention (which we adopt), the electron affinity is positive if energy is released when the electron attaches to the atom (that is, Eea > 0 implies that electron attachment is exothermic). It follows from a similar argument to that given in the Justification above that the standard enthalpy of electron gain, ∆egHo, at a temperature T is related to the electron affinity by
∆egHo(T) =−Eea – 5/2RT
Note the change of sign. In typical thermodynamic cycles the 5–2RT that appears in eqn 10.35 cancels that in eqn 10.34, so ionization energies and electron affinities can be used directly. A final preliminary point is that the electron-gain enthalpy of a species X is the negative of the ionization enthalpy of its negative ion:
∆egHo(X) =−∆ionHo(X−)
As ionization energy is often easier to measure than electron affinity, this relation can be used to determine numerical values of the latter. As will be familiar from introductory chemistry, ionization energies and electron affinities show periodicities. The former is more regular and we concentrate on it. Lithium has a low first ionization energy because its outermost electron is well shielded from the nucleus by the core (Zeff = 1.3, compared with Z = 3). The ionization energy of beryllium (Z = 4) is greater but that of boron is lower because in the latter the outermost electron occupies a 2p orbital and is less strongly bound than if it had been a 2s electron. The ionization energy increases from boron to nitrogen on account of the increasing nuclear charge. However, the ionization energy of oxygen is less than would be expected by simple extrapolation. The explanation is that at oxygen a 2p orbital must become doubly occupied, and the electron–electron repulsions are increased above what would be expected by simple extrapolation along the row. In addition, the loss of a 2p electron results in a configuration with a half-filled subshell (like that of N), which is an arrangement of low energy, so the energy of O+ + e− is lower than might be expected, and the ionization energy is correspondingly low too. (The kink is less pronounced in the next row, between phosphorus and sulfur because their orbitals are more diffuse.) The values for oxygen, fluorine, and neon fall roughly on the same line, the increase of their ionization energies reflecting the increasing attraction of the more highly charged nuclei for the outermost electrons.
The outermost electron in sodium is 3s. It is far from the nucleus, and the latter’s charge is shielded by the compact, complete neon-like core. As a result, the ionization energy of sodium is substantially lower than that of neon. The periodic cycle starts again along this row, and the variation of the ionization energy can be traced to similar reasons. Electron affinities are greatest close to fluorine, for the incoming electron enters a vacancy in a compact valence shell and can interact strongly with the nucleus. The attachment of an electron to an anion (as in the formation of O2− from O−) is invariably endothermic, so Eea is negative. The incoming electron is repelled by the charge already present. Electron affinities are also small, and may be negative, when an electron enters an orbital that is far from the nucleus (as in the heavier alkali metal atoms) or is forced by the Pauli principle to occupy a new shell (as in the noble gas atoms).
الاكثر قراءة في مواضيع عامة في الكيمياء الفيزيائية
اخر الاخبار
اخبار العتبة العباسية المقدسة
